Partitioning A Hexagon
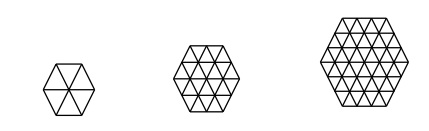
Following the pattern of the first 3 figures above, how many little triangles are there in the 9 th figure?
The answer is 486.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
THE PROBLEM SHOULD HV SPECIFIED THAT ONLY THE SMALLEST TRIANGES ARE TO BE TAKEN IN ACCOUNT... NOT OTHERWISE.. tHERE ARE MANY BIGGER TRIANGES THAT ARE FORMED ASWELL.. WHICH ENDS UP IN MULTIPLES OF 6
Log in to reply
Read the question carefully, it says "how many little triangles are there in the 9th figure?"
i'm glad someone else thinks like that
Take a deep breath, turn off caps lock, then reread the problem.
accually your problem would be way crazier
This is my favourite solution.
Very great thax this was a simple way to explain
subscribe to pewdie pie and help youtube live youtube.com
Log in to reply
me loves pewdiepie but not on math problems
mira como la tengo dura por ti 8-----)
Lol I did the same thing
Where did 2n+2n-5, 2n+2n-3, and 2n+2n-1 come from?
Log in to reply
1, 3, 5, 7, ... , 2n-5, 2n-3, 2n-1 are odd numbers from 1 to 2n-1
I don't understand this!
Woah, that's impressive
Pattern #1 includes 6 triangles.
Pattern #2 includes 24 triangles.
Pattern #3 includes 54 triangles.
We can notice right off the bat that all three of these numbers are divisible by 6.
When we divide each number by 6, we get the following sequence: 1, 4, 9
1, 4, and 9 are 1 2 , 2 2 , and 3 2 , respectively.
Therefore, we can conclude that the pattern can be described by the following equation: x = 6 n 2
Since we're looking at the ninth item in the sequence: ( 6 ) 9 2 = 4 8 6
Most helpful by far! Well done
Another solution is to find the series of how many tiles are added to the outside as each layer is added.
By observation the first three layers have 6 ⋅ 1 , 6 ⋅ 3 , and 6 ⋅ 5 added to the outside of the previous level (6 sides to the shape times 2 i − 1 triangles added per side on the i th later), leading to to the total tiles at each level being the sum of tiles added up to that point:
∑ i = 1 n 6 ⋅ ( 2 i − 1 ) which is equivalent to 6 ∑ i = 1 n ( 2 i − 1 ) where n is the number of layers.
Using the formula for the sum of a series, ∑ i = 1 n a i = 2 n ( a 1 + a n ) , this gives:
6 ∑ i = 1 9 ( 2 i − 1 ) = 6 ⋅ ( 2 9 ( 1 + 1 7 ) ) = 6 ⋅ 9 ⋅ 9 = 6 ⋅ 8 1 = 4 8 6
Each picture is made of 6 larger triangles, which each equal to n squared. Or, n squared x 6. 9 squared x 6 is 486 triangles total.
A hexagon can be cut into 6 triangles. I will refer to these as sectors to minimize confusion. The pattern goes that you square the placement of the hexagon (first hexagon = 1, second hexagon =2, etc) to find the number of triangles within a sector of the hexagon. So, for example, the first hexagon can be broken up into 6 triangles. It's placement is first, so you square 1. 6*(1^2) = 6 triangles (first shape)
The pattern continues:
6 (2^2)=24 triangles (second shape).... 6 (3^2) triangles = 54 triangles (third shape)...
To answer the question:
6*(9^2) triangles = 486 triangles
486 is the correct answer
I observed the first 3 iterations:
6,24,54 and came up with an easy solution:
suppose iteration = n, so we can make a function:
P(n)=6*n^2
6*9^2=486
This question is easy, how come only 46% got it right?
the hexagon can be dissected into 6 big triangles, the n t h triangle have 2 sequence of triangles, the upside one ( 1 + 2 + . . . + n ) and the downside one 1 + 2 + . . . + ( n − 1 ) .
so, total small triangles will be: 6 ∗ ( 2 n ∗ ( n + 1 ) + 2 n ∗ ( n − 1 ) ) = 6 ∗ 2 n ∗ ( n 2 − 1 )
by substituting n = 9 , you will get 4 8 6
I got the solution to write yay, let me explain how, you can notice that the hexagon contains 6 different (big)triangles for each triangle you can calculate the (little)triangles by noticing that it's the sum of the first n odd numbers ( n = 1 − > S = 1 , n = 2 − > S = 1 + 3 = 4 , n = 3 − > S = 1 + 3 + 5 = 9 . . e t c ) if you would notice the sum(S) always equals n 2 there is a simple proof for this find it any were online you might also know this if you study number theory but if you couldn't notice the pattern you could have easily calculated the sum of the first n odd numbers.
- at n = 9 (ie the 9th pattern)
- no. small triangles in a big triangle ( S ) = n 2 = 9 2 = 8 1
- no. small triangles in the hexagon = no. big triangles in a hexagon ∗ S = 6 ∗ 8 1 = 4 8 6
a challenge that would be interesting: what is the total number of triangles (any size) in the Nth figure
hint: start by solving it for the 9th figure
The formula to get the number of little triangles on the n t h figure is 6 ∗ n 2 .
Plugging 9 in place of n gives 6 ∗ 9 2 = 4 8 6 , which is our answer.
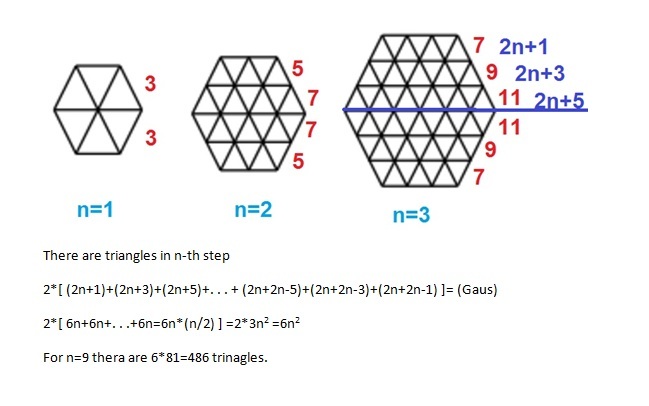
Every picture can be subdivided into six equal regions which contain exactly n 2 triangles each; thus, the ninth picture will have 6 ∗ 9 2 = 4 8 6 triangles in total.