A number theory problem by Paul Ryan Longhas
The number above shows the concatenation of positive integers between 10 and 99 (inclusive), denote that value as .
What is the remainder when is divided by 99?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Moderator note:
Great. For clarity, you should explain how you calculated .
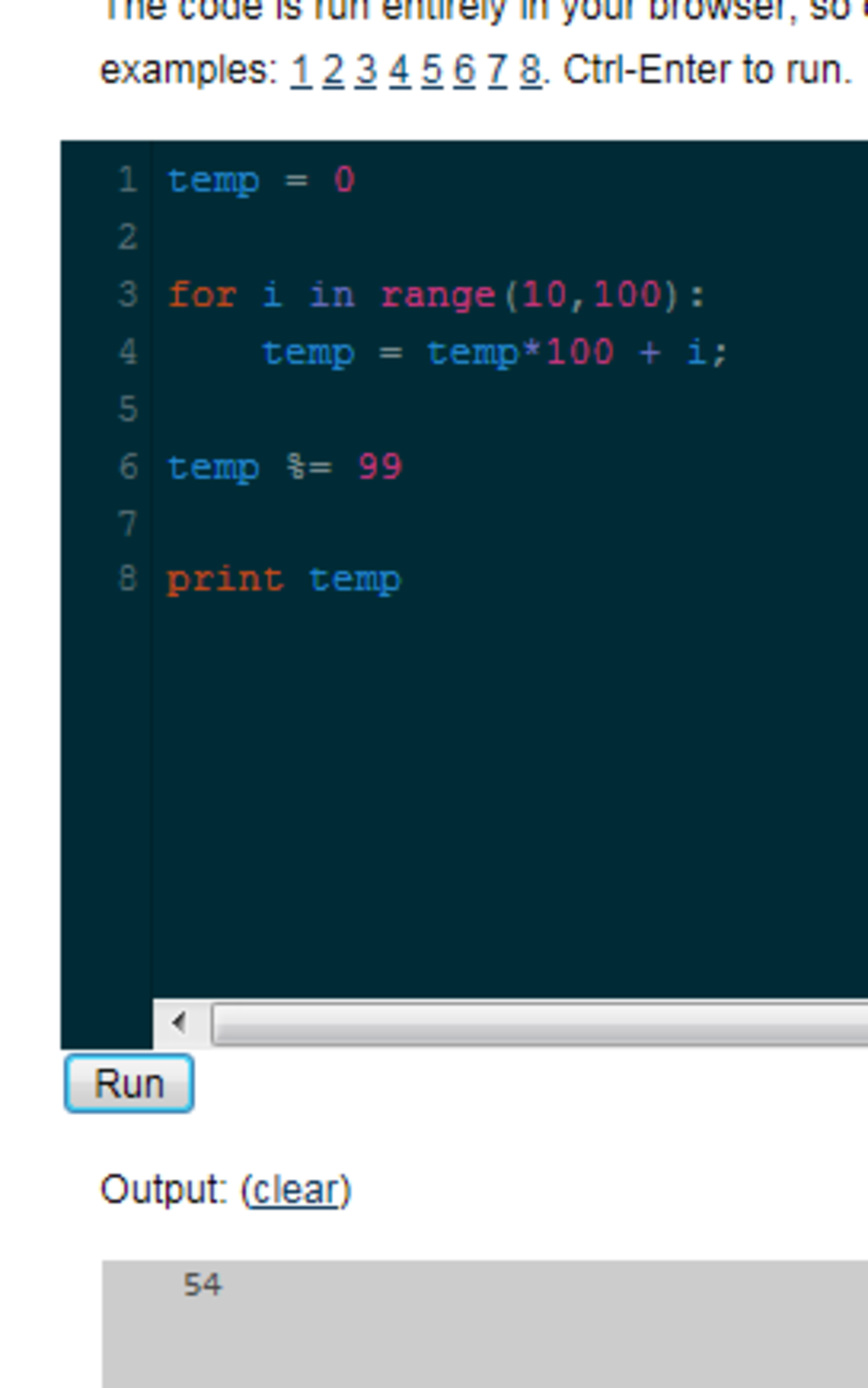
N = 99 + 98 10^2 + 97 10^4 + ....... and so on. Notice that 99 mod 99 = 0 ;
98*10^2 mod 99 = 98 ;
97*10^4 mod 99 = 97 ; ...... and so on. Now , add them up ... remainder = 98 + 97 + ... + 10 =4905 ;
Divide 4905 by 99 to obtain 54 as remainder