An algebra problem by Wildan Bagus Wicaksono
Find the value of
( 3 2 0 1 8 ) 2 − ( 3 2 0 1 6 ) 2 ( 3 2 0 1 7 ) 2 − ( 3 2 0 1 5 ) 2 .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
Verified with a calculator, 1/9th is the answer.
Log in to reply
Thanks for pointing it out. We have accidentally changed the answer. I've updated the answer. Those who previously answered 9 1 has been marked correct.
Wolfram Alpha also agrees.
Frankly this is looking like at least 26% got this wrong. 1/9 by my reckoning.
Log in to reply
Thanks for pointing it out. We have accidentally changed the answer. I've updated the answer. Those who previously answered 9 1 has been marked correct.
I also got 1/9 as the answer, why 1/3?
I got 1/9, not 1/3
Log in to reply
Thanks for pointing it out. We have accidentally changed the answer. I've updated the answer. Those who previously answered 9 1 has been marked correct.
Dude, there a typo in 3rd step
This is the same exact answer i got , why is it wrong !?
The answer is 1/9 so why is it wrong?
Log in to reply
Thanks for pointing it out. We have accidentally changed the answer. I've updated the answer. Those who previously answered 9 1 has been marked correct.
I got 1/9. Explain to me how the answer is 1/3.
Log in to reply
Thanks for pointing it out. We have accidentally changed the answer. I've updated the answer. Those who previously answered 9 1 has been marked correct.
The answer is 9 1 .
Log in to reply
Thanks for pointing it out. We have accidentally changed the answer. I've updated the answer. Those who previously answered 9 1 has been marked correct.
the answer is 1/9 , why is it incorrect
Log in to reply
Thanks for pointing it out. We have accidentally changed the answer. I've updated the answer. Those who previously answered 9 1 has been marked correct.
26% of people got this right :)
In step 3 we can take out 3 4 0 3 0 common, leaving 3 6 − 3 2 3 4 − 1 which gives 7 2 0 8 0 , simplifying to 9 1
Log in to reply
As I recall that time, I gave the key 1/9 and many answered correctly. But why change? Previously I apologized. But I remember I locked the answer is 1/9.
Thee is typo I second step
As I recall that time, I gave the key 1/9 and many answered correctly. But why change?
I got 1/9 as well.
Log in to reply
As I recall that time, I gave the key 1/9 and many answered correctly. But why change? Previously I apologized. But I remember I locked the answer is 1/9.
The answer is 1/9
Log in to reply
As I recall that time, I gave the key 1/9 and many answered correctly. But why change? Previously I apologized. But I remember I locked the answer is 1/9.
Log in to reply
Thanks for pointing it out. We have accidentally changed the answer. I've updated the answer. Those who previously answered 9 1 has been marked correct.
To website admin: it's pretty confusing when you answer a question correctly and get told it's wrong by the webpage. Kinda makes me not want to participate any more :(
Log in to reply
Yes, BUT - I've been here for a few years every day and this is the FIRST TIME I've ever seen this happen. So, don't worry!
Log in to reply
Thanks for pointing it out. We have accidentally changed the answer. I've updated the answer. Those who previously answered 9 1 has been marked correct.
What is wrong with this problem? The answer is 1/9, this is the correct answer (i solved it by hand using two different ways and checked it in wolfram alpha to be sure). Why the problem says that the answer is 1/3?
Log in to reply
Thanks for pointing it out. We have accidentally changed the answer. I've updated the answer. Those who previously answered 9 1 has been marked correct.
1/9 is the answer
I came up with 1/1. Because 3 to the 4036 power minus 3 to the 4032 power is 3 to the 4th power which is 81 for the numerator The denominator is also 3 to the 4th power which is 81 and 81 over 81 is 1
This question is solved in the best possible way
Just in the last formula turn 10to30. "-,4034 , -- , (4010<4030),"
Log in to reply
As I recall that time, I gave the key 1/9 and many answered correctly. But why change? Previously I apologized. But I remember I locked the answer is 1/9.
L e t u = 2 0 1 5 And then plug into the expression: = ( 3 u + 3 ) 2 − ( 3 u + 1 ) 2 ( 3 u + 2 ) 2 − ( 3 u ) 2 = 3 2 u × 3 6 − 3 2 u × 3 2 3 2 u × 3 4 − 3 2 u = 3 2 u ( 3 6 − 3 2 ) 3 2 u ( 3 4 − 1 ) = 3 2 + 4 − 3 2 3 4 − 1 = 3 2 × 3 4 − 3 2 3 4 − 1 = 3 2 ( 3 4 − 1 ) ( 3 4 − 1 ) = 3 2 1 = 9 1
( 3 2 0 1 8 ) 2 − ( 3 2 0 1 6 ) 2 ( 3 2 0 1 7 ) 2 − ( 3 2 0 1 5 ) 2 = 3 4 0 3 6 − 3 4 0 3 2 3 4 0 3 4 − 3 4 0 3 0 = 3 4 0 3 2 ( 3 4 − 1 ) 3 4 0 3 0 ( 3 4 − 1 ) = 3 2 1 = 9 1
I would have expanded your denominator to 9(x^2-y^2), and we can eliminate both (x^2-y^2), so there isn't a need to apply a^2-b^2 = (a-b)(a+b).
( 3 2 0 1 8 ) 2 − ( 3 2 0 1 6 ) 2 ( 3 2 0 1 7 ) 2 − ( 3 2 0 1 5 ) 2 = 3 2 ∗ ( 3 2 0 1 7 ) 2 − 3 2 ∗ ( 3 2 0 1 5 ) 2 ( 3 2 0 1 7 ) 2 − ( 3 2 0 1 5 ) 2 = 3 2 1 ∗ ( 3 2 0 1 7 ) 2 − ( 3 2 0 1 5 ) 2 ( 3 2 0 1 7 ) 2 − ( 3 2 0 1 5 ) 2 = 3 2 1 = 9 1
I'm a firm believer in avoiding unnecessary computations.
I'm a firm believer in avoiding unnecessary computations.
Yup, that's an important motto to be a good mathematician! =D
Initial expression:
( 3 2 0 1 8 ) 2 − ( 3 2 0 1 6 ) 2 ( 3 2 0 1 7 ) 2 − ( 3 2 0 1 5 ) 2
Apply Difference of Squares
( 3 2 0 1 8 + 3 2 0 1 6 ) ( 3 2 0 1 8 − 3 2 0 1 6 ) ( 3 2 0 1 7 + 3 2 0 1 5 ) ( 3 2 0 1 7 − 3 2 0 1 5 )
Divide each term by 3 2 0 1 5
3 2 0 1 5 ( 3 3 + 3 1 ) ( 3 3 − 3 1 ) 3 2 0 1 5 ( 3 2 + 3 0 ) ( 3 2 − 3 0 )
Simplify
( 2 7 + 3 ) ( 2 7 − 3 ) ( 9 + 1 ) ( 9 − 1 )
Simplify, Simplify
( 3 0 ) ( 2 4 ) ( 1 0 ) ( 8 ) = ( 3 ) ( 3 ) ( 1 ) ( 1 ) = 9 1
I made x=3^2015 . Then boils down to (81x^2-x^2)/(279x^2-9x^2)=1/9 . Much like others above. Would perhaps have been better to make x=(3^2015)^2 . Good ole retrospectoscope.
Take (3^2015)^2 common on numerator and denominator then over the both you'll get (81➖ 1)➗ (729➖ 9)= 80/720= 1/9
LaTex: We notice that the common factor is : ( 3 2 0 1 5 ) 2
LaTex: ( 3 2 0 1 8 ) 2 − ( 3 2 0 1 6 ) 2 ( 3 2 0 1 7 ) 2 − ( 3 2 0 1 5 ) 2 = ( 3 2 0 1 5 ) 2 ⋅ ( 3 6 ) − ( 3 2 0 1 5 ) 2 ⋅ ( 3 2 ) ( 3 2 0 1 5 ) 2 ⋅ ( 3 4 ) − ( 3 2 0 1 5 ) 2
LaTex: ( 3 2 0 1 8 ) 2 − ( 3 2 0 1 6 ) 2 ( 3 2 0 1 7 ) 2 − ( 3 2 0 1 5 ) 2 = ( 3 2 0 1 5 ) 2 ⋅ ( ( 3 4 ) − 1 ) ⋅ ( 3 2 ) ( 3 2 0 1 5 ) 2 ⋅ ⎝ ⎛ ( 3 4 ) − 1 ⎠ ⎞
LaTex: ( 3 2 0 1 8 ) 2 − ( 3 2 0 1 6 ) 2 ( 3 2 0 1 7 ) 2 − ( 3 2 0 1 5 ) 2 = 3 2 1 = 9 1
[(3^2017)²-(3^2015)²]/[(3^2018)²-(3^2016)²] a²-b²= (a+b)(a-b) =[(3^2017+3^2015)(3^2017-3^2015)] / [(3^2018+3^2016)(3^2018-3^2016)] =[3^2015(3²+1)3^2015(3²-1)] / [3^2016(3²+1)3^2016(3^2-1) Notebook = 3²-1 and 3²+1 habis dibagi =3^2015+2015-2016-2016 =3^-2 =1/3² =1/9 Just it.. Thank you 😀
If you take a factor of 3 2 out of the denominator, you end up with the numerator.
Put 3^2015=k by substituting in the expression( (k×9)^2-k^2)÷((k×27)^2-(k×3)^2) expression=(81-1)÷(27^2-3^2)=80÷(30×24)=1÷9##
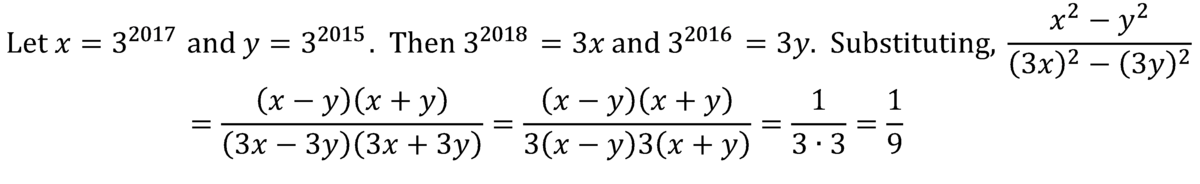
Relevant wiki: Rules of Exponents
= ( 3 2 0 1 8 ) 2 − ( 3 2 0 1 6 ) 2 ( 3 2 0 1 7 ) 2 − ( 3 2 0 1 5 ) 2 = 3 4 0 3 6 − 3 4 0 3 2 3 4 0 3 4 − 3 4 0 3 0 = 3 2 ( 3 4 0 3 4 − 3 4 0 3 0 ) 3 4 0 3 4 − 3 4 0 3 0 = 9 1