A palindrome problem!
What is the number of palindromes which have 2 x digits,where x > 0 . If the answer is of the form, A × B x − C ,where A , B , C are positive integers and A is as small as it can be,then what is the value of A + B + C ?
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
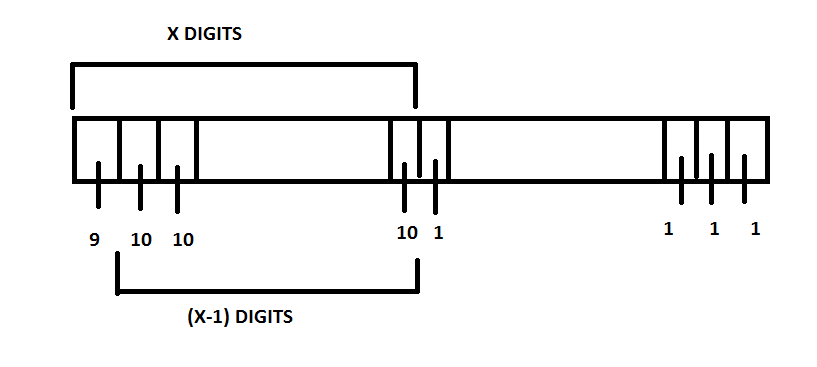 From the above image we have that the total number of palindromes of
2
x
digits
=
9
×
1
0
x
−
1
,hence
A
=
9
,
B
=
1
0
,
C
=
1
⟹
A
+
B
+
C
=
2
0
.And done!
From the above image we have that the total number of palindromes of
2
x
digits
=
9
×
1
0
x
−
1
,hence
A
=
9
,
B
=
1
0
,
C
=
1
⟹
A
+
B
+
C
=
2
0
.And done!
Moderator note:
Are those values of A , B , C uniquely determined? Why can't there be other such triplets?
Nice diagram ! Upvoted :).
I am really sorry sir,I have made the required corrections.
If F ( x ) = A × B x − C = 9 × 1 0 x − 1 , then F ( 0 ) F ( 1 ) = B = 1 0 And F ( 0 ) = A × 1 0 − C = 9 × 1 0 − 1 A = 9 × 1 0 C − 1 The smallest integer value for A is A = 9 , C = 1