A parabola with a twist
The parabola y = a x 2 with a = 1 6 1 , is given a twist of 5 π clockwise, then it is translated such that it becomes tangent to the x and y axes, in the first quadrant, as shown below. Find the area bounded by the x -axis , the y -axis, and the parabola (shaded in light blue).
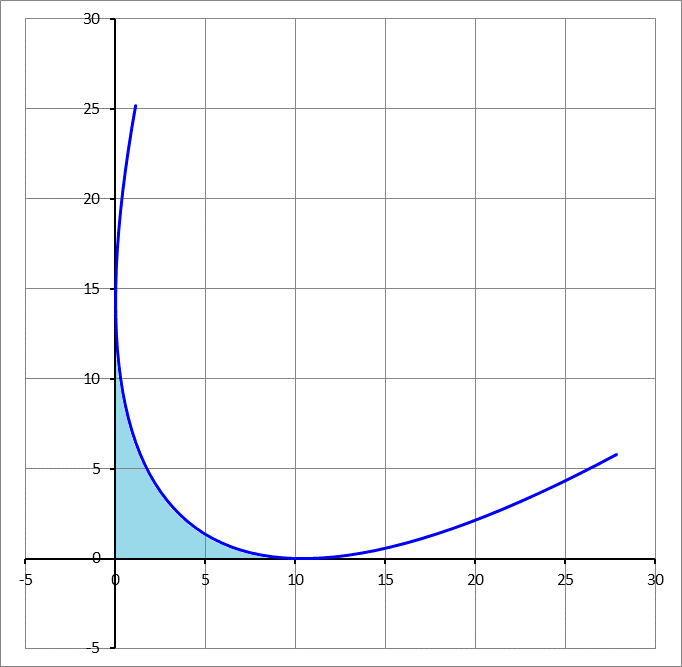
The answer is 24.8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
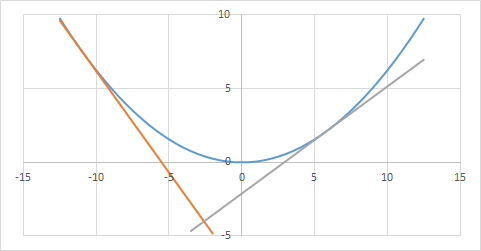
Retaining the original x - and y -axes of the parabola y = a x 2 , the graphs are as shown above. Instead of the parabola tilts 5 π clockwise, it is equivalent to the new x ′ -axis (orange line) tilts 5 π anticlockwise. Instead of the parabola translates up and to the right, the x ′ -axis translates down and to the left until it is tangent to the parabola.
Therefore, x ′ -axis has a gradient of − cot 5 π and so is the point on the parabola it is tangent to. Since the gradient of the parabola is d x d y = 2 a x = 8 x = − cot 5 π , ⟹ x = − 8 cot 5 π and y = a x 2 = 4 cot 2 5 π . Therefore, the point of tangent is ( − 8 cot 5 π , 4 cot 2 5 π ) . From x + 8 cot 5 π y − 4 cot 2 5 π = − cot 5 π , the equation of x ′ -axis is y = − x cot 5 π − 4 cot 2 5 π .
The y ′ -axis (grey line) is perpendicular to x ′ -axis, hence it has a gradient of tan 5 π . The point of tangent is ( 8 tan 5 π , 4 tan 2 5 π ) and the equation of y ′ -axis is y = x tan 5 π − 4 tan 2 5 π .
From − x cot 5 π − 4 cot 2 5 π = x tan 5 π − 4 tan 2 5 π , we find that x ′ -axis and y ′ -axis intersect at x = 4 ( tan 5 π − cot 5 π ) .
Then the area bounded by the parabola, x ′ -axis, and y ′ -axis is given by:
A = ∫ 4 ( tan 5 π − cot 5 π ) 8 tan 5 π ( a x 2 − ( x tan 5 π − 4 tan 2 5 π ) ) d x + ∫ − 8 cot 5 π 4 ( tan 5 π − cot 5 π ) ( a x 2 − ( − x cot 5 π − 4 cot 2 5 π ) ) d x = ∫ − 8 cot 5 π 8 tan 5 π 1 6 x 2 d x − ∫ 4 ( tan 5 π − cot 5 π ) 8 tan 5 π ( x tan 5 π − 4 tan 2 5 π ) d x + ∫ − 8 cot 5 π 4 ( tan 5 π − cot 5 π ) ( x cot 5 π + 4 cot 2 5 π ) d x = 4 8 x 3 ∣ ∣ ∣ ∣ − 8 cot 5 π 8 tan 5 π − [ 2 x 2 tan 5 π − 4 x tan 2 5 π ] 4 ( tan 5 π − cot 5 π ) 8 tan 5 π + [ 2 x 2 cot 5 π + 4 x cot 2 5 π ] − 8 cot 5 π 4 ( tan 5 π − cot 5 π ) ≈ 2 4 . 7 9 9
The parametric equation of the parabola is,
r ( t ) = d + R [ t , a t 2 ] T ( 1 )
where
R = R ( θ ) = [ cos θ sin θ − sin θ cos θ ] ( 2 )
(our angle of rotation θ = − 5 π ) and d = [ d x , d y ] T is the coordinate vector of the vertex. The parameter is t ∈ R .
The tangent to the parabola is obtained by differentiating r ( t ) with respect to t ,
r ′ ( t ) = R [ 1 , 2 a t ] T ( 3 )
Expanding the right hand side of (3), yields,
r ′ ( t ) = [ c − 2 a t s , s + 2 a t c ] T ( 4 )
where c = cos θ , and s = sin θ .
Setting the y-coordinate of r ′ ( t ) to 0 (horizontal tangent), yields
t 1 = − 2 a 1 tan θ > 0 ( 5 ) ,
and setting the x-coordinate of r ′ ( t ) to 0 (vertical tangent), yields
t 2 = 2 a 1 cot θ < 0 ( 6 )
Further, at t 1 , the y-coordinate is zero, so
d y + [ 0 , 1 ] R [ t 1 , a t 1 2 ] T = 0 ( 7 )
and at t 2 , the x-coordinate is zero, so that,
d x + [ 1 , 0 ] R [ t 2 , a t 2 2 ] T = 0 ( 8 )
hence, we have found the vertex d . (You can check that d x = 4 . 4 5 4 0 6 5 4 5 8 ,and d y = 1 . 7 0 8 2 0 3 9 3 )
The area bounded by a parametric curve p ( t ) = [ x ( t ) , y ( t ) ] T over the interval [ t 1 , t 2 ] and the line segments connecting the origin with p ( t 1 ) and the origin with p ( t 2 ) is given by the famous formula,
A = 2 1 ∣ ∣ ∣ ∣ ∫ t 1 t 2 ( x ( t ) y ′ ( t ) − x ′ ( t ) y ( t ) ) d t ∣ ∣ ∣ ∣ ( 9 )
For our curve,
x ( t ) = d x + c t − a s t 2
y ( t ) = d y + s t + a c t 2
And, the derivatives are,
x ′ ( t ) = c − 2 a s t
y ′ ( t ) = s + 2 a c t
Plugging this into the above formula gives,
A = 2 1 ∣ ∣ ∣ ∣ ∫ t 1 t 2 ( ( d x + c t − a s t 2 ) ( s + 2 a c t ) − ( d y + s t + a c t 2 ) ( c − 2 a s t ) ) d t ∣ ∣ ∣ ∣
Expanding, simplifying and re-arranging, this becomes,
A = 2 1 ∣ ∣ ∣ ∣ ∫ t 1 t 2 ( ( s d x − c d y ) + 2 a t ( c d x + s d y ) + a t 2 ) ) d t ∣ ∣ ∣ ∣
Now this is straightforward to integrate, and it evaluates to ≈ 2 4 . 8
Any area bounded by the x -axis, y -axis, and a parabola in the form of y = a x 2 that is rotated by θ and translated so that it becomes tangent to the x and y axes is always 6 1 the area of the rectangle defined by origin and the two tangent points, no matter what the value of a or θ is. The proof is as follows:
Instead of rotating the parabola y = a x 2 , rotate the x - and y - axes by θ instead, and draw rectangle A D B E defined by the origin and the two tangent points, and draw parallelogram A B F G so that F G is tangent to the parabola at C and B F and A G are parallel to the y -axis.
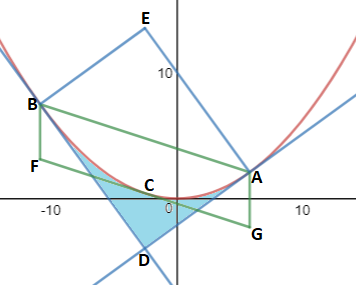
The rotated x -axis has a slope of tan θ and the rotated y -axis has a slope of − cot θ . The slopes of the parabola y = a x 2 is defined by m = y ′ = 2 a x , so at A it is 2 a x = tan θ and this solves to coordinates A ( 2 a tan θ , 4 a tan 2 θ ) , and at B it is 2 a x = − cot θ and this solves to coordinates B ( − 2 a cot θ , 4 a cot 2 θ ) . The rotated x -axis follows a line with the equation y − 4 a tan 2 θ = tan θ ( x − 2 a tan θ ) and the rotated y -axis follows a line with the equation y − 4 a cot 2 θ = − cot θ ( x − 2 a cot θ ) , which intersects at D ( 4 a tan θ − cot θ , − 4 a 1 ) . Using these coordinates and the distance formula, segment A D has a length of 4 a sin θ cos 2 θ 1 and segment B D has a length of 4 a sin 2 θ cos θ 1 , which means rectangle A D B E has an area of A A D B E = 1 6 a 2 sin 3 θ cos 3 θ 1 .
Using the slope formula, the slope between A and B is 2 1 ( tan θ − cot θ ) , and the equation of the line along A B is y − 2 a tan θ = 2 1 ( tan θ − cot θ ) ( x − 4 a tan 2 θ ) or y = 2 1 ( tan θ − cot θ ) x + 4 a 1 . The slopes of the parabola y = a x 2 is defined by m = y ′ = 2 a x , so at C it is 2 a x = 2 1 ( tan θ − cot θ ) and this solves to coordinates C ( 4 a tan θ − cot θ , 1 6 a ( tan θ − cot θ ) 2 ) . The equation of the line along F G through C is y − 1 6 a ( tan θ − cot θ ) 2 = 2 1 ( tan θ − cot θ ) ( x − 4 a tan θ − cot θ ) or y = 2 1 ( tan θ − cot θ ) x − 1 6 a ( tan θ − cot θ ) 2 . The height of parallelogram A B F G is the difference of the y -intercepts of the lines along A B and F G , which is h A B F G = 4 a 1 − − 1 6 a ( tan θ − cot θ ) 2 = 1 6 a sin 2 θ cos 2 θ 1 . The base of parallelogram A B F G is the difference of the x -coordinates of A and B , which is b A B F G = 2 a tan θ − 2 a cot θ = 2 a sin θ cos θ 1 . The area of parallelogram A B F G is A A B F G = b A B F G ⋅ h A B F G = 3 2 a 2 sin 3 θ cos 3 θ 1 , so the area of the region in the parabola enclosed by the parallelogram is A p a r a = 3 2 A A B F G = 4 8 a 2 sin 3 θ cos 3 θ 1 = 3 1 A A D B E .
The area of the shaded region is the difference between the area of △ A D B E and the parabola enclosed by parallelogram A B F G , or A s = 2 1 A A D B E − 3 1 A A D B E = 6 1 A A D B E = 9 6 a 2 sin 3 θ cos 3 θ 1 . Therefore, the area bounded by the x -axis, y -axis, and a parabola in the form of y = a x 2 that is rotated by θ and translated so that it becomes tangent to the x and y axes is always 6 1 the area of the rectangle defined by origin and the two tangent points.
In this problem, a = 1 6 1 and θ = 5 π , so the area of the shaded region is A s = 9 6 ( 1 6 1 ) 2 sin 3 5 π cos 3 5 π 1 ≈ 2 4 . 8 .
Instead of finding a formula for the rotated parabola, we can just rotate the x and y axes instead.
One of the axes when rotated by 5 π will have a slope of tan 5 π (it doesn't matter whether this is positive or negative as the parabola is symmetrical). For simplicity, let this be the constant t = tan 5 π . The other axis, which is perpendicular, will have a slope of − t 1 .
Now we need to find the lines with these slopes that are tangent to the parabola. To do this, we will differentiate the parabola to get y ′ = 8 x , and substitute in the required slopes:
t x 1 y 1 y − y 1 y − 4 t 2 y − 4 t 2 y = 8 x 1 = 8 t = 1 6 ( 8 t ) 2 = 4 t 2 = m ( x − x 1 ) = t ( x − 8 t ) = t x − 8 t 2 = t x − 4 t 2 − t 1 x 2 y 2 y − y 2 y − t 2 4 y − t 2 4 y = 8 x 2 = − t 8 = 1 6 ( − t 8 ) 2 = t 2 4 = m ( x − x 2 ) = − t 1 ( x + t 8 ) = − t 1 x − t 2 8 = − t x − t 2 4
We already know that these lines intersect the parabola at x 1 = 8 t and x 2 = − t 8 respectively. Lastly, we need their intersection point:
t x − 4 t 2 x t + t x x ( t + t 1 ) x = − t x − t 2 4 = 4 t 2 − t 2 4 = 4 ( t + t 1 ) ( t − t 1 ) = 4 ( t − t 1 )
Now we can use these x-coordinates as the terminals to integrals between the parabola and the lines to find the total area:
Area = ∫ − t 8 4 ( t − t 1 ) 1 6 x 2 − ( − t x − t 2 4 ) d x + ∫ 4 ( t − t 1 ) 8 t 1 6 x 2 − ( t x − 4 t 2 ) d x
Evaluating these integrals gives Area ≈ 2 4 . 8 .