A Parallelogram and 2 Circles
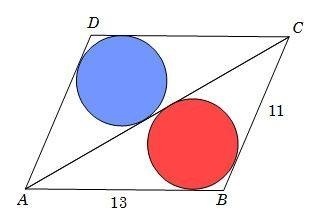In Parallelogram ABCD,
A
B
=
1
3
,
B
C
=
1
1
, and
A
C
=
2
0
. Two congruent circles are inscribed in
△
A
C
D
and
△
A
C
B
as shown in the figure.
The shortest distance between the centers of the two inscribed circles can be expressed in the form a b . Where b is a square-free integer. Find the value of a + b .
- Found this somewhere.
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
would you please explain the part 1 3 − ( 2 0 / 2 + x ) = 1 1 − ( 2 0 / 2 − x ) .
Log in to reply
I think it is a typo. 1 3 2 − ( 2 0 / 2 + x ) 2 = 1 1 2 − ( 2 0 / 2 − x ) 2
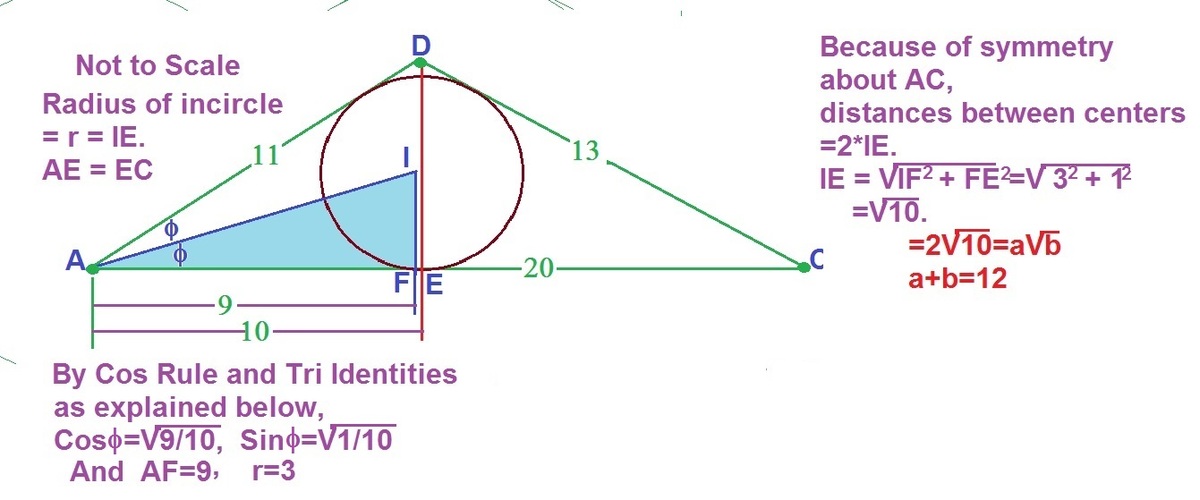
C o s 2 ϕ = 2 ∗ 1 1 ∗ 2 0 1 1 2 + 2 0 2 − 1 3 2 = 5 4 . C o s ϕ = 2 1 ∗ ( C o s 2 ϕ + 1 ) = 1 0 9 , S i n ϕ = 1 0 1 r = P e r i m e t e r 2 ∗ A r e a = 1 1 + 1 3 + 2 0 2 ∗ 4 1 ∗ 4 4 ∗ 2 2 ∗ 1 8 ∗ 4 = 3 . I F / A F = 3 / A F = C o s ϕ S i n ϕ , ∴ A F = 3 ∗ 3 = 9 .
p = ( A B + B C + A C ) / 2 = ( 1 3 + 1 1 + 2 0 ) / 2 = 2 2 .
r =congruent circle radius
r = ( ( p − A B ) ( p − B C ) ( p − A C ) / p ) 1 / 2 = ( ( 2 2 − 1 3 ) ( 2 2 − 1 1 ) ( 2 2 − 2 0 ) / 2 2 ) 1 / 2 = 3 .
d =The shortest distance between the centeres
x=distance between center of AC and the intersection point of perpendicular line from center of circle to AC which is also the radius of circle
( d / 2 ) 2 = x 2 + r 2 .
( d / 2 ) 2 = x 2 + 9 .
On the other hand :
1 3 − ( 2 0 / 2 + x ) = 1 1 − ( 2 0 / 2 − x ) .
x = 1 .
Therefore :
( d / 2 ) 2 = 1 + 9 = 1 0 .
d = 2 X ( 1 0 ) 1 / 2 .
a = 2 , b = 1 0 .
a + b = 2 + 1 0 = 1 2 .