A parity path

We can start by trying out few paths, just for examining properties of the board. Soon, we can see that board is designed in such a way that it's impossible to go from start to finish crossing even number just by randomly going from one vertex to another: we always end up with odd crossed lines. Our goal is to make a strategy, look for shapes formed by vertices which could fix our parity problem.

We see that crossing one line two times doesn't change anything, which is logical: if $n$ is the number of lines crossed from beginning, at some vertex, then after going to neighboring vertex and back number of lines crossed will be now $n+2$ , thus parity of crossed lines won't change (see picture).

"Odd" and "even" by each vertex show the parity of lines crossed from beginning.

But, what if we had another vertex between these two, a vertex which is connected to both of them, but does not lie on the same line as these two (they are non-collinear)? In that way, we can fix our parity problem! (Look at the picture)

Actually, every polygon with $odd$ number of sides would help, and conversely any polygon with $even$ number of sides wouldn't. All we should do is to find a triangle in this "web of lines", find a shortest path from start to it, go around its sides (fixing parity problem) and then find the shortest path to finish. That's similar path to the one which Djordje showed in his solution (his path goes around pentagon) and takes minimum $\boxed{18}$ lines to cross to complete it.

A walk is an alternating sequence of nodes (dots) and edges (line segments) starting and ending at a node, where each edge connects the nodes it is between in the sequence. The length of a walk is the number of its edges. The problem requires finding a walk between node S ("START") and F ("FINISH") whose length is smallest and even.

Starting with node F, node-color the graph, i.e., assign a color to each node so that no two neighboring nodes have the same color : F is orange, it's neighbors are black, their neighbors are orange, and so on - see left figure. Only two colors are needed until the 3-cycle (triangle LRB) is reached, where one additional color (blue) is required because each of the triangle's 3 nodes is a neighbor of the other two. There are 3 cases to consider, depending on which triangle node is colored blue.

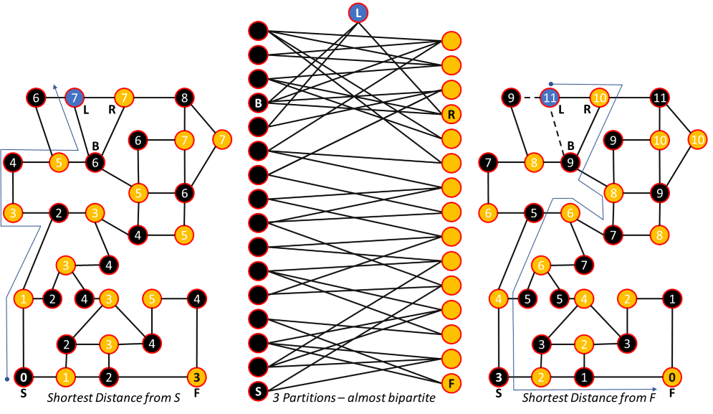
Case 1 - L is blue: The node coloring allows tracking the length parity of any walk because each color partition (set of colored nodes) has the property that no nodes of the same color are neighbors - see center figure. So, the length parity of any walk that starts and ends on a black node that goes only through black and yellow nodes is always even, no matter how long the walk. Similarly for any black and yellow walk with both ends on a yellow. For any black and yellow walk with one end on a black and the other on a yellow, the length parity is odd. Therefore, since nodes S and F have opposite color, any black and yellow walk between them will have odd parity.

However, the 3-node sequence black $\rightarrow$ blue $\rightarrow$ yellow (or its reverse) has length 2 so its parity is even. Hence, an even parity walk between S and F that is shortest can be constructed by finding a shortest path (no node or edge repeats in the walk sequence) between S and L, and then finding a shortest path between L and F as long as the 2nd node in the L $\rightarrow$ F path and the next-to-last node of the S $\rightarrow$ L path have different colors (black and yellow).

Shortest paths can be quickly found by hand using the Dijkstra algorithm . The shortest path distance from S to every node is shown as a number inside each node in the left figure. To find a feasible shortest L $\rightarrow$ F path, only allow edges from L that connect to nodes having a color different from the next-to-last node of the S $\rightarrow$ L path. These are shown as non-broken edges in the right figure where also shown are the shortest distances from F to every node as a number inside each node. Therefore, length(S $\rightarrow$ L) + length(L $\rightarrow$ F) = 7 + 11 = 18 .

Case 2 - R is blue: Switching colors of nodes L and R in the left figure constructs a valid node coloring, and the analysis is the same as Case 1 $\Rightarrow$ shortest even S $\rightarrow$ F walk length is 18 .

Case 3 - B is blue: Instead of explicitly constructing a valid node coloring (which is forced to have multiple blue nodes), we argue that any even walk for this case can't be any shorter than 18. For if an even walk could be shorter, it cannot include both nodes L and R because a shortest even walk using both of those nodes has already been found in the previous cases. However, any S $\rightarrow$ F walk that goes through at most one of the nodes L or R is necessarily odd, as the explicit coloring in Case 1 (left figure) or Case 2 shows.

Therefore, the shortest even S $\rightarrow$ F walk has length $\boxed{18}$ .

Note: a shortest even S $\rightarrow$ F walk is not unique. An example walk is shown in the figures, different from Djordje's for variety.

(QUESTION: How many distinct shortest even S $\rightarrow$ F walks are there?)

@Djordje Veljkovic- interesting, thought-provoking problem. Thanx for that.