A particle spiraling in a magnetic field
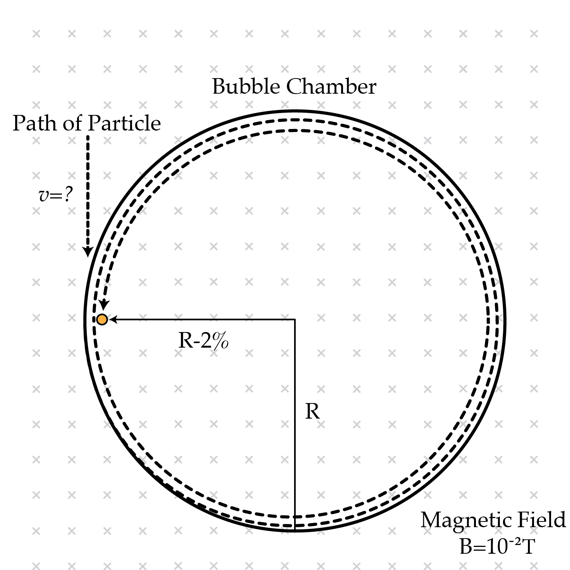
A particle with specific charge α : = m q = 1 0 8 C/kg enters a bubble chamber where its path can be observed. A magnetic field of induction B = 1 0 − 2 T is perpendicular to the particle's velocity. The particle experiences a viscous drag force which is approximately proportional to its velocity, that is F d r a g = − k v . As a consequence of this force, the particle spirals inward. It is observed that after two full rotations the radius of curvature decreases by 2 % . Then the magnetic field is switched off and the particle travels L = 3 0 cm before coming to a stop. What was the particle's velocity in m/s right before entering the chamber?
The answer is 487.2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
How can u say that the total distance travelled is 4πR. It means that the particle continuously travelled in a circle without any radial inward motion
From the equality of the magnetic centripetal force against the centrifugal force we get: For initial entry velocity Vi and exit velocity Ve from the chamber: q/m=Vi/(RixB)=Ve/(RexB), where Ri-initial radius and Re exit radius and given Ri/Re=1/0.98=1.02. Now: Fdrag=-KxV and a(acceleration)=dv/dt=-KxV/m or dt=(dV/V(-K/m)) and set m/K=z integrating on both sides will give Ve=Vixexp(-t/z) The way the particle makes in the chamber before stopping the Mag. field is approx 4xPi(Ri+Re)/2 or two complete rotations with an average radius of AVG{Ri,Re}. On the other hand the distance can be computed from the integral of the momentary speeds around the circles: S=INT{VixExp(-t/z)} which equals to 4xPi(Ri+Re)/2 All I get Vixz(1-exp(-t/z))=4xPi(Ri+Re)/2 assuming the lower time limit=0 it is not hard to see that we get Vixz-Vexz=4Pix(m/q)x(1/B)(Vi+Ve)/2 when using the relations between the radii to the speeds. Transfer it to the form 1.02xVexz-Vexz where 1.02=1/0.98 Vexz=The stopping distance in our case 0.3meter which we get from the equation S=Vexzx(1-exp(-t/z)) by sustitution of t=infinite or S=Vexz=0.3meter in this case From now on just a hard long work to place the different items in place and get the final solution. finally for short Vexz(or 0.3)*(1.02-1)=4xPix(m/q)x(1/B)xVix(1+0.98)x(1/2) out of which we can compute Vi the speed of the particle when entering the chamber.
motion of the particle after switching off the magnetic field:
m \frac {dv}{dt} = - k v
by the solution of the differential equation we obtain
v {t} = v {0} e^(-kt/m) (1)
\frac {dx}{dt} = v_{0} e^(-kt/m)
by solving the differential equation again, we obtain
x = - v \frac {m}{k e^(kt/m)} + v \frac {m}{k}
when the particle comes to stop , time is infinity
substituting obtains v_{0} = 0.3 \frac {k}{m} (2)
motion while rotating:
qvB = m \frac {v^2}{r}
by substituting we obtain the following:
in the beginning of rotation : r = \frac {v_{0}}{10^6}
in the end of rotation : r = \frac {v {t}}{r(1-2%)} = \frac {v {t}}{r \times 0.96*10^6}
\frac {v_{0}}{v(t)} = \frac {1}{0.98)}
while \frac {qB}{m} = \frac {v}{r}
then, the angular velocity is always constant
t = \frac {theta}{omega}
t = \frac {4 * pi}{10^6} = 1.256637 \times 10^-5 second
using equation (1), but while rotating, we obtain
v {t} = v {0} e^(-kt/m) (3)
\frac {v_{0}}{v(t)} = e^(kt/m)
\frac {1}{0.98)} = e^(\frac {1}{0.98)} * 1.256637 \times 10^-5)
by solving the equation we obtain
\frac {k}{m} = 1607.6804
we know that v {0} in equation (2) equals v {t} in equation (3)
so we obtain
0.3 \frac {k}{m} = v_{0} e^(-kt/m)
after solving the equation we can get the value of v_{0}
v_{0} = 492.147 m/s
Since the radius of curvature changes gradually we can write m R v 2 = q v B → R = α B v . Therefore, a small change of the particle's velocity ( Δ v ) implies a small change of the radius R ( Δ R ). From the last equation we have that R Δ R = v Δ v ≈ v 0 Δ v → v 0 Δ v = − ϵ where ϵ = 2 / 1 0 0 . Thus the velocity of the particle after two rotations is v 1 = v 0 ( 1 − ϵ ) . When the magnetic field is switched off, Newton's second Law assumes the form m d t d v = − k v → m d t d v = − k d t d s → m ∫ d v = − k ∫ d s which implies v 1 = m k L → v 0 ( 1 − ϵ ) = m k L . In order to solve the problem we need an additional equation. Note that m d t d v = − k v → m ∫ d v = − k ∫ d s can also be applied when the particle is spiraling inward. Then it yields m Δ v = − k s = − k 4 π R and since R = α B v we arrive at the relation ϵ = m k α B 4 π Now we can get rid of the unknown ratio m k to obtain v 0 = 4 π ( 1 − ϵ ) α B ϵ L = 4 8 7 . 2 m/s .
Let the initial velocity of the particle before entering the magnetic field be v and let its velocity just after the magnetic field is switched off be u.Basically, we need to find v. Initial radius = R = frac{m * v}{B * q} Final radius = 0.98 * R = frac{m * u}{B * q} Thus, dividing the two equations, we get u = 0.98 * v Given that drag force F = m a = - k v , where v is velocity of the particle at that instant. We know that a = v * frac{dv}{dx}
Integrating the above equation with v varying from v to u and x varying from 0 to 4 \pi R , we get m (u-v) = - k * 4 \pi R. Substituting u = 0.98 * v, we get frac{k}{m} = frac{0.02 * v}{4 \pi R}. Now, integrate the force equation with velocity varying from u to 0 and distance x varying from 0 to L, we get frac{k}{m} = frac{u}{L}. Substituting the values of u, L and frac{k}{m} in this equation, we can find R to be equal to 0.000487 metres. But, R = frac{m * v}{B * q} Thus, substituting the values R, B and frac{q}{m}, we get v = 487.2 m/s.