A physically unrealizable problem
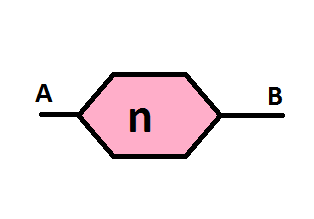
 Let us define a
hexaresistor
(depicted below)
Let us define a
hexaresistor
(depicted below)
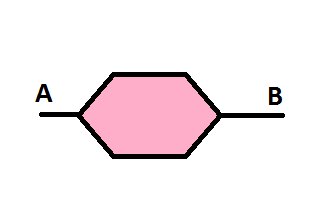
as a hexagonal resistive network which can be described as below:
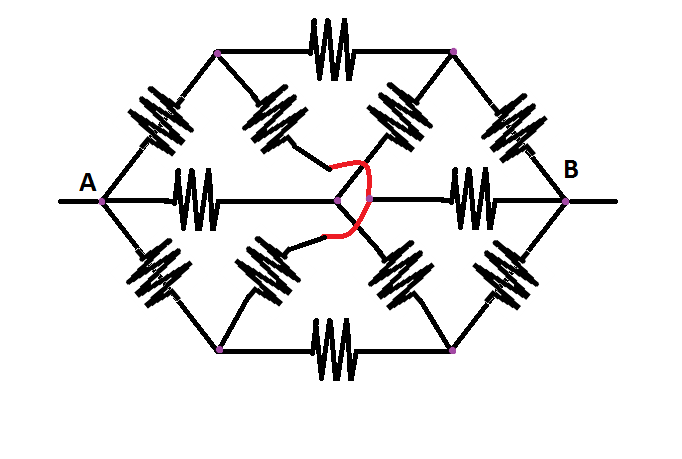
with all the resistors having a value of R .
Then, let us define a second order hexaresistor (depicted below)
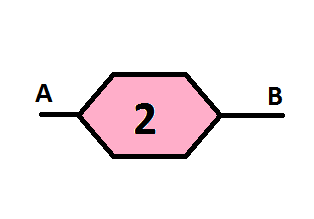
as a network which can be described as a hexagonal resistive network of hexaresistors as shown below:
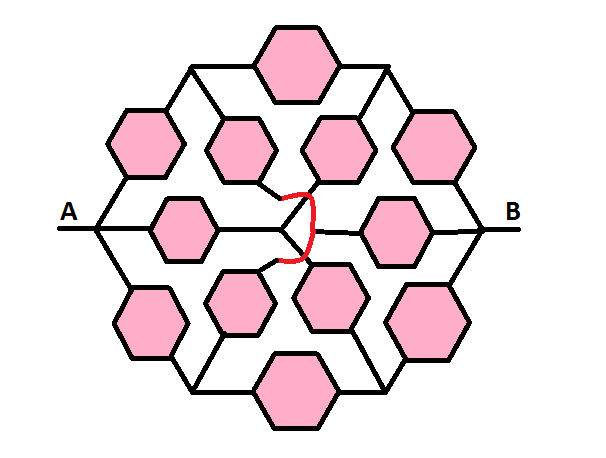
If we construct an identical hexagonal resistive network of second order hexaresistors, we will be able to create a third order hexaresistor , and so on, such that an n-order hexaresistor , depicted below
is a network of
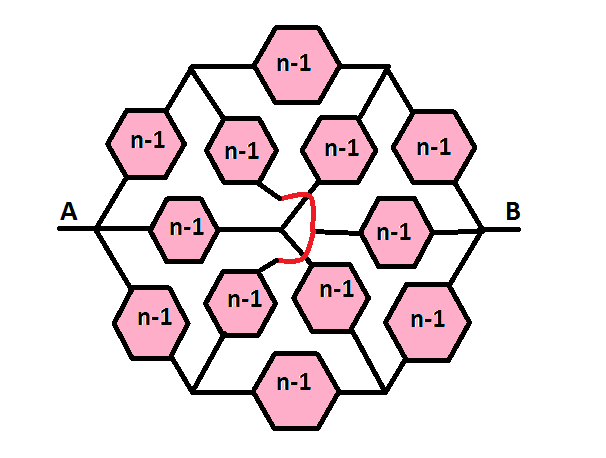 .
.
If R = 1000 ohms, determine the resistance from points A to B, where B extends to infinity.
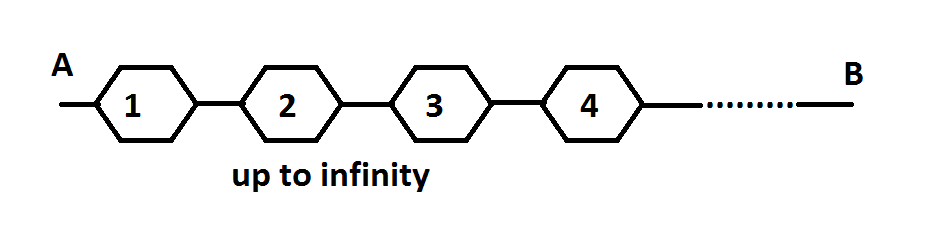
Note : This is physically unrealizable, but theoretically, a particular value is approached.
The answer is 5000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Same solution. Amazzzzzing question.
A beauty of coincidence!
Each R at the 4 corners are converted from R into 2 R // 2 R as the very first start!
We obtain a proposed equivalent circuit of 4 main parallels yet to be verified as follows:
|---- 2 R -- ∗ - R ---- ∗ --- 2 R ----| [1] |~~~~~~---- R - ∗ -- 2 R ----|
|---- R ---- |~~~~~~~~~| [2]
|~~~~~~---- R -#-- 2 R ----| |---- 2 R -- ∗ - R ----~~~~~~|
|~~~~~~~~~|---- R ----| [3]
|---- 2 R --#- R ----~~~~~~| |---- 2 R ---#---- R -#-- 2 R ----| [4]
Note that "~" is a sign I applied as a push, it stands for a space. 2 detached points ∗ , and 2 detached points # changed into 4 × ∗ and 4 × #respectively.
With test voltage of 5 V on rail on our left, and 0 V on rail on our right, let's see partial circuits [1] and [2]:
[ 1 ] : 5 V → 3 V → 2 V → 0 V as 2 R + R + 2 R 2 R 5 V = 2 V
[ 2 ] : 5 V → 3 V → 2 V → 0 V as R + 1 . 5 R 1 . 5 R 5 V = 3 V and R + 2 R 2 R 3 V = 2 V
The coincidence here is 2 V onto detached points between [1] and [2] and also same detached points between [3] and [4] are allowed as there shall be no current to flow between them no matter there are contacts or not, because of same voltage or zero potential difference!
Consequently, we have obtained 5 R // 2.5 R // 2.5 R // 5 R which is 5 1 + 2 . 5 1 + 2 . 5 1 + 5 1 1 R = 6 5 R
R<1> = 1000 Ω × 6 5 = 8 3 3 3 1 Ω
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
|
The above is R<1>, R<2>, R<3>, R<4>, ..., R<300>; before R< ∞ >, it has approached to 0 Ω !
Each of which multiplied by 6 5 for each step of resistance followed.
Sum of R<i> from 1 to ∞ = 1000 1 − 6 5 6 5 Ω = 5000 Ω
Answer: 5 0 0 0
what an amazing question..... really took me some time to figure out :)
Considering the above figure as a cube having each resistor of R Ω and a voltage source of E M F ( V ) connected across A and B .
V = I R A B
By applying Kirchhoff's laws on loop A C D B A ,
V = 3 I R + 6 I R + 3 I R I R A B = I R ( 3 2 + 6 1 ) R A B = 6 5 R
So, we can get the R e q for 1-order hexaresistor as ( 6 5 ) 1 0 0 0 Ω .
And 2-order hexareaistor will have R e q as ( 6 5 ) 2 1 0 0 0 Ω .
And so on.
So our answer is as follows,
= ( 6 5 ) 1 0 0 0 + ( 6 5 ) 2 1 0 0 0 + ( 6 5 ) 3 1 0 0 0 + … = 1 0 0 0 ( 1 − 6 5 6 5 ) = 1 0 0 0 × 5 = 5 0 0 0