A Planar Cut Through an Ellipsoid
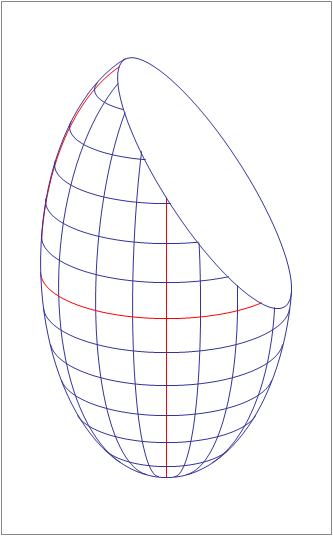 An ellipsoid with center
and semi-axes of lengths 10, 15, and 30 along the
and
directions, respectively, is cut by a plane whose equation is
.
An ellipsoid with center
and semi-axes of lengths 10, 15, and 30 along the
and
directions, respectively, is cut by a plane whose equation is
.
The intersection of the ellipsoid and the plane is an ellipse.
Find its area.
This problem is original.
The answer is 503.717.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The equation of the given ellipsoid is
a 2 x 2 + b 2 y 2 + c 2 z 2 = 1
where
a = 1 0 , b = 1 5 , c = 3 0
Define
r = [ x , y , z ] T
Then the equation of the ellipsoid can be written as
r T B r = 1
where
B = ⎣ ⎡ a 2 1 0 0 0 b 2 1 0 0 0 c 2 1 ⎦ ⎤
On the other hand, a point in the cutting plane can be written in parametric form as
r = r 0 + V u
where r 0 is the position vector of any point on the plane, and matrix V is composed of two columns of two vectors v 1 and v 2 that are perpendicular to the normal vector to the plane. Further we will take v 1 and v 2 to be perpendicular to each other and to be of unit length.
The normal to the given plane is
n = [ 1 , 3 , 2 ] T
So I chose
v 1 = 5 1 [ − 2 , 0 , 1 ] T
and
v 2 = n ^ × v 1
where n ^ is the normalized version of n.
Now we can substitute the equation of the plane into the equation of the ellipsoid
( r 0 + V u ) T B ( r 0 + V u ) = 1
Expanding
r 0 T B r 0 + u T V T B V u + 2 u T V T B r 0 = 1
Rearranging
u T V T B V u + 2 u T V T B r 0 = 1 − r 0 T B r 0
Now the left hand side can be written as
( u + u 0 ) T V T B V ( u + u 0 ) − u 0 T V T B V u 0
where
u 0 = ( V T B V ) − 1 V T B r 0
Finally, set
u = R w − u 0
where R is the orthonormal matrix of the normalized eigenvectors of V T B V . Using this change of variables, we arrive at
w T D w = 1 − r 0 T B r 0 + u 0 T V T B V u 0
where D is the diagonal matrix resulting from diagonalization of V T B V through R .
Dividing by the right hand side gives the standard equation of the ellipse
w T E w = 1
where
E = D / ( 1 − r 0 T B r 0 + u 0 T V T B V u 0 )
Now the diagonal entries of E are the reciprocals of the squares of the lengths of the semi-minor and semi-major axes.
Doing the necessary calculations, gives the following values for semi-axes
a = 8 . 6 8 4 8 , b = 1 8 . 4 6 1 9
The area of the ellipse is given by
A = π a b = 5 0 3 . 7 1 7