A planar cut through an Elliptical Cylinder
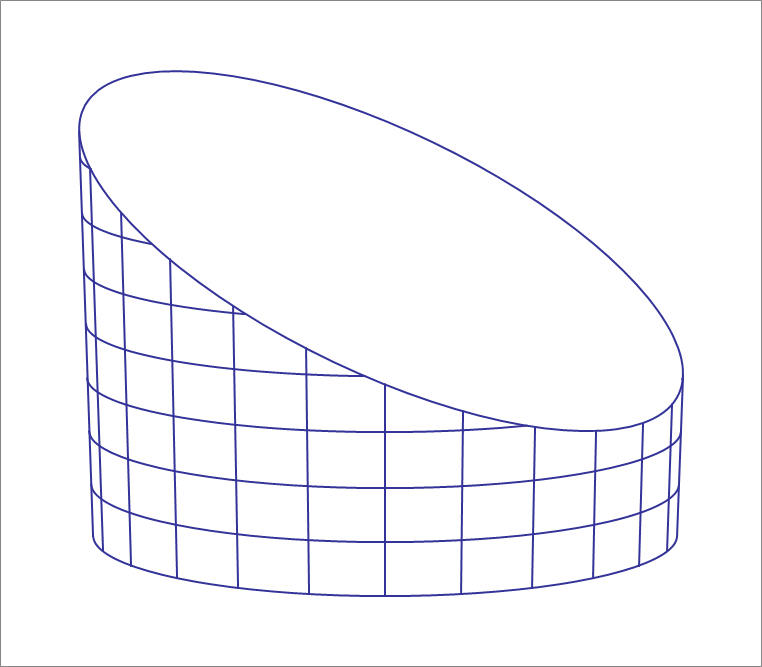
A right cylinder whose axis is along the -axis, has an elliptical cross-section (in the horizontal plane) given above.
If a plane whose equation is , cuts through the cylinder, then the cutting plane and the cylinder intersect in an ellipse. Find the sum of the semi-minor and semi-major axes of this ellipse.
Round your answer to three decimal places.
The answer is 26.937.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The equation of an elliptical cylinder, can be written in vector-matrix form as
r T Q r = 1
where r = [ x , y , z ] T , and
Q = ⎣ ⎡ 1 / a 2 0 0 0 1 / b 2 0 0 0 0 ⎦ ⎤
And the cutting plane vector equation is r = r 0 + V u , where V = [ v 1 , v 2 ] is a 3 x 2 matrix, whose columns v 1 and v 2 are two unit vectors orthogonal to each other and to the normal to the plane.
Therefore,
( r 0 + V u ) T Q ( r 0 + V u ) = 1
u T V T Q V u + 2 r 0 T Q V u = 1 − r 0 T Q r 0
( u − u 0 ) T V T Q V ( u − u 0 ) = c
where u 0 = − ( V T Q V ) − 1 V T Q r 0 and c = 1 − r 0 T Q r 0 + u 0 T V T Q V u 0
Let B = ( 1 / c ) V T Q V , then
( u − u 0 ) T B ( u − u 0 ) = 1
Next we diagonalize matrix B, by finding a rotation matrix R , and a diagonal matrix D, such that
R T B R = D
hence, if we make the change of coordinate, u = R w + u 0 , then
w T D w = 1
which is the well-known equation of an ellipse, given that the diagonal entries of D are positive, which is the case.
Hence the ellipse in the w-plane, and consequently in the u-plane, has semi-major and semi-minor axes equal to the reciprocal of the square roots of the diagonal entries of D.
Performing the calculations, results in a semi-minor axis m = 1 0 . 6 0 6 6 and a semi-major axis M = 1 6 . 3 2 9 9 3 , making the answer M + m = 2 6 . 9 3 7 .