A Planar Cut through an Oblique Cone
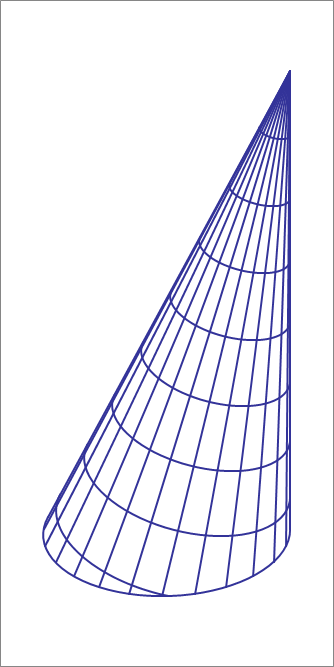
An oblique cone has a circular base centered at the origin of radius 5, and an apex at . A plane whose equation is cuts through the oblique cone, and the resulting cut is an ellipse. Then the semi-minor and semi-major axes lengths are:
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Vectors connecting the apex to points on the base along the lateral curved surface of the cone are given by
v ( t ) = ( 5 cos t , 5 sin t − 5 , − 2 0 )
All the other points on the surface of the cone are scalar multiples of these vectors plus an offset of the apex coordinates.
We can think of this cone as a linear transformation of another arbitrary standard right circular cone.
Note first that v ( t ) can be written as
v ( t ) = cos t ( 5 , 0 , 0 ) + sin t ( 0 , 5 , 0 ) + ( 0 , − 5 , − 2 0 ) = v 1 cos t + v 2 sin t + v 0
An arbitrary standard right circular cone with apex at the origin, and a circular base centered at ( 0 , 0 , − h ) , and radius of base r has the following form of its lateral vectors
u ( t ) = cos t ( r , 0 , 0 ) + sin t ( 0 , r , 0 ) + ( 0 , 0 , − h ) = u 1 cos t + u 2 sin t + u 0
So we can write the vectors ( 5 , 0 , 0 ) , ( 0 , 5 , 0 ) , ( 0 , − 5 , − 2 0 ) (which are v 1 , v 2 , v 0 ) as a linear transformation (matrix multiplication) of
the vectors ( r , 0 , 0 ) , ( 0 , r , 0 ) , and ( 0 , 0 , − h ) , ( which are u 1 , u 2 , u 0 )
i.e. we set the matrix equation,
V = A U
where V = [ v 1 v 2 v 0 ] and U = [ u 1 u 2 u 0 ]
The solution for A is simply A = V U − 1
For computation, we can take h = 1 , r = 1 . It follows that points on our oblique cone are given by r = r 0 + A r ′ , where r 0 is the apex of the oblique cone, and r ′ is the position vector of a point on the right circular cone. Now, we know that the algebraic equation of points on the right circular cone are given by r ′ T Q ′ r ′ = 0 , where for the simple choice that we made of h = 1 , and r = 1 , we have,
Q ′ = ⎣ ⎡ 1 0 0 0 1 0 0 0 − 1 ⎦ ⎤
Substituting for r ′ , we obtain,
( A − 1 ( r − r 0 ) ) T Q ′ ( A − 1 ( r − r 0 ) ) = 0
which simplifies to,
( r − r 0 ) T Q ( r − r 0 ) = 0 where Q = A − T Q ′ A − 1
Now, we are ready to intersect this oblique cone with the plane. The vector equation of the plane is
r = r 1 + W u
where r 1 is any point on the plane, and W = [ w 1 , w 2 ] is a 3 × 2 matrix whose columns are arbitrary unit vectors that together with the normal to the plane form an orthonormal basis for R 3 .
Substituting this vector expression into the equation of the oblique cone, one obtains,
( r 1 − r 0 + W u ) T Q ( r 1 − r 0 + W u ) = 0
Expanding this quadratic form gives,
u T ( W T Q W ) u + 2 u T W T Q ( r 1 − r 0 ) + ( r 1 − r 0 ) T Q ( r 1 − r 0 ) = 0
Take u 0 = − ( W T Q W ) − 1 W T Q ( r 1 − r 0 ) , then the above equation becomes,
( u − u 0 ) T ( W T Q W ) ( u − u 0 ) = C
where the constant C is given by C = − ( r 1 − r 0 ) T Q ( r 1 − r 0 ) + u 0 T ( W T Q W ) u 0
Dividing by C , we obtain,
( u − u 0 ) T Q 1 ( u − u 0 ) = 1
where Q 1 = C 1 ( W T Q W ) .
The final step is to diagonalize Q 1 into Q 1 = R D R T . The diagonal elements the diagonal matrix D are the eigenvalues of Q 1 which are the reciprocal of the square of the semi-minor and semi-major axes lengths of the resulting ellipse of intersection.
Note that depending the orientation of the cutting plane, the intersection can also be parabolic or hyperbolic.