A plane cutting through a paraboloid

Geometry Level 5

A paraboloid is given by

z = 0.25 x 2 + 0.1 y 2 z = 0.25 x^2 + 0.1 y^2

It is cut by a plane passing through ( 10 , 10 , 20 ) (10, 10, 20) with a unit normal of ( 1 2 , 1 2 , − 1 2 ) ( \frac{1}{2}, \frac{1}{2}, -\frac{1}{\sqrt{2}} ) . The resulting cut is an ellipse as the animation below shows. Find the sum of the semi-minor and semi-major axes of this ellipse.


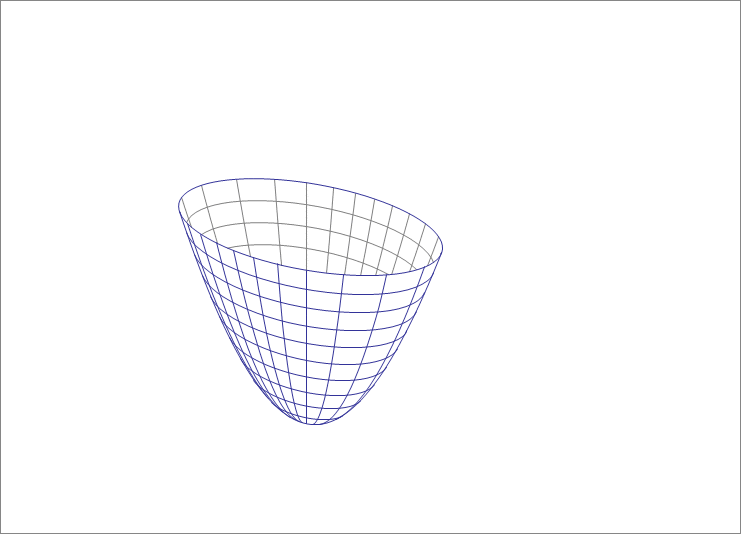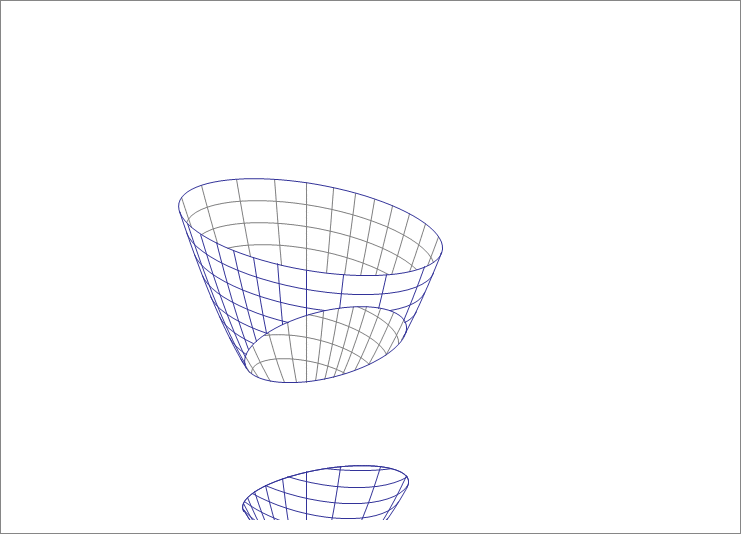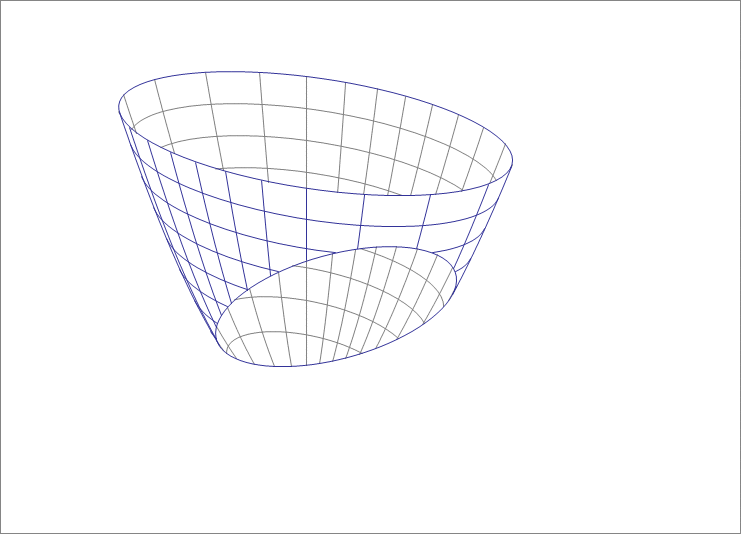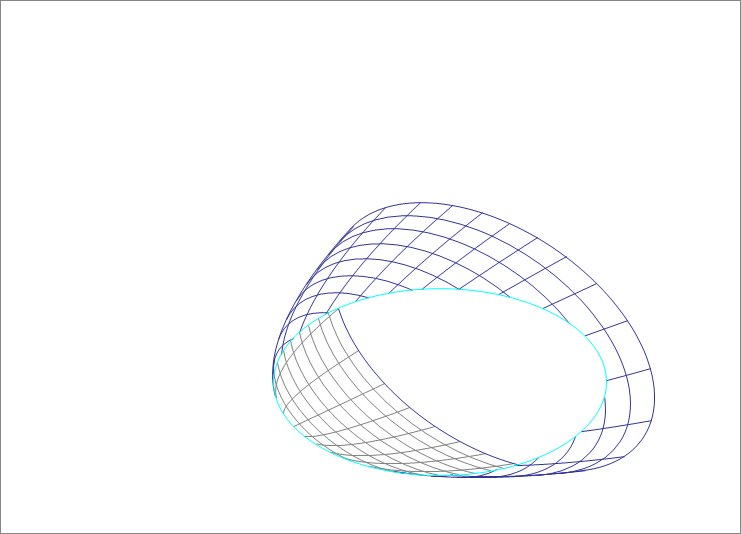
The answer is 17.2.

Hosam Hajjir by Hosam Hajjir , 56, Canada

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Yuriy Kazakov
Feb 16, 2020

I use Mathcad and approach Ellipse in Space - 2

I find the parametric equations for ellipse line.

The curvature is given by κ = ∥ f ′ × f ′ ′ ∥ ∥ f ′ ∥ 3 \kappa = \dfrac{\lVert f' \times f'' \rVert}{\lVert f' \rVert^3}

​

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...