A plus overlapped on a square

Geometry Level 3

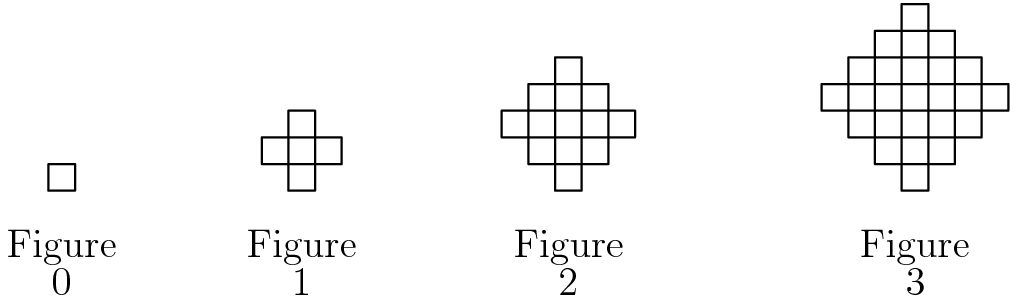
Figures 0. 1, 2 and 3 consist of 1, 5, 13 and 25 non-overlapping unit squares respectively. If the pattern were continued, how many non-overlapping unit squares would be there in figure 100 ?

20201 10401 19801 40801 39801

1 solution

Anish Harsha
Mar 24, 2016

We can divide up the figure $n$ to get the sum of the first $n+1$ odd numbers and the sum of first $n$ odd numbers. If you don't see this, here is the example for $n=3$ .

The sum of first $n$ odd numbers is $n^2$ , so for figure $n$ , there are $(n+1)^2 + n^2$ unit squares. We plug in $n=100$ to get $(100+1)^2+100^2$ unit squares, which is $20201$ .

@Anish Harsha you should write the source also :)

sanyam goel - 5 years, 2 months ago

In general, the nth figure has n^2 +(n+1)^2 non-overlapping squares.

Daniel Xian - 2 years, 4 months ago

A plus overlapped on a square

1 solution

0 pending reports