A point in a quadrilateral
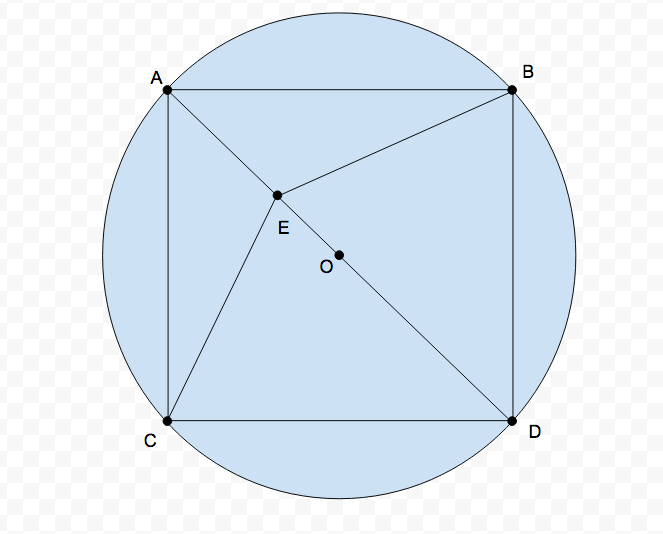
The figure above shows cyclic quadrilateral inscribed in circle , whose diagonals are congruent and share the same midpoint. A point is chosen, where is inside the quadrilateral. Let , , and the circumference of the circle be . Also, . Determine the perimeter of triangle . Round your answer to the nearest thousandth. A scientific calculator is allowed.
Note: the figure is not to scale.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The first step is to solve for x , where − 2 x + 1 0 . 5 = x 2 − 4 x + 7 . 5 . The solutions are − 1 and 3 , but − 1 is negative, so 3 is the solution. After substituting the value 3 into ( 2 x + 1 ) for the length of C E , a system of equations can be formed using the Pythagorean Theorem relating B D , D C , and A D , Stewart's Theorem relating B D , A B , A E , E D , and B E , and the British Flag theorem relating C E , B E , A E , and E D . These equations can be used to determine B E , E D , and B D , where the values can be added to determine the perimeter of triangle B E D for a final answer of 1 8 . 7 6 4 .