A Polygon Flower

Geometry Level 5

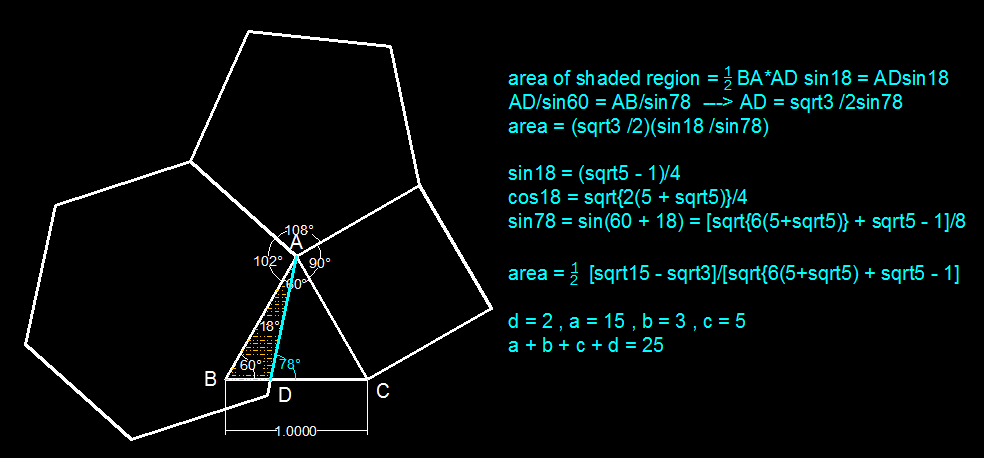
Regular Polygons are arranged around a unit equilateral triangle as shown in the figure above.

If the hatched area can be written as $\frac{1}{d} \frac{\sqrt{a}-\sqrt{b}}{\sqrt{3d(\sqrt{c}+c)}+\sqrt{c}-1}$ for square-free integers $a, b, c$ and $d$ . Find $a+b+c+d$ .

The answer is 25.

1 solution

Ahmad Saad
Jan 8, 2016

@Digvijay Singh and @ahmad saad do you think this problem is over rated? If one knows the value of $\sin 18$ then he/she can solve the question easily.

Akshay Yadav - 5 years, 5 months ago

Yes, It wasn't a hard nut to crack. Just simple trigonomerty and geometry.

It must've been rated Level 4.

Edit: It is rated Level 4 now.

Digvijay Singh - 5 years, 5 months ago

I had solved it differently so I didn't get it in that exact form you wanted, so I couldn't answer the question as an integer. Maybe allow the actual area (rounded to some decimals) as an answer to allow for different solutions.

I essentially treated AB as the x axis. line AD would be y=tan(18)x and BC is y=-tan(60)x +root3.

the height of the intersection of those 2 lines is the height of the triangle. from which I get area. maybe a bit primitive but it works.. i think.

Aren Nercessian - 5 years, 5 months ago

A Polygon Flower

The answer is 25.

1 solution

0 pending reports