Resistance through a 3D Polyhedron

Relevant wiki: Transformation of Resistances (Star to Delta and Delta to Star)

If you apply Delta-wye Transformation on every point where three lines intersect, and combining parellel lines through each edge , suprizingly you will get an icosahedron, with a resistance of $r=\frac{3}{5} \Omega$ between any two adjascent nodes.

Now observe, that by symmetry the potentials at points $G,C,D,E,F$ are equal. So no current will flow from $GC,CD,DE,EF,FG$ .

So we can join the points $G,C,D,E,F$ .

Similarly, the potentials at $H,I,J,K,L$ are equal. So no current will flow from $HI,IJ,JK,KL,LH.$ So these points can also be joined.

So the circuit simplifies to:-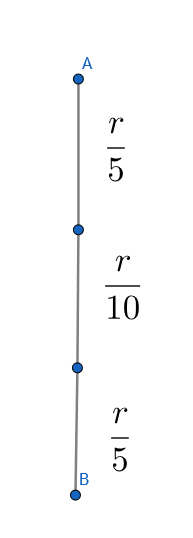 Now from A to B, the resistances are in series, so adding them gives $R=\frac{1}{2} r$

We know that $r=\frac{3}{5} \Omega.$

So putting this we get $R=\boxed{\frac{3}{10}\Omega}$ . So the answer is $\boxed{30}$