A Pre-RMO question! -11

Label the unknowns as in the Venn diagram above. Then we have:

$\begin{cases} a+ d=45 &...(1) \\ a+ c = 30 &...(2) \\ a+ b = 8 &...(3) \\ a+ c + d = 80-9=71 &...(4) \end{cases}$

From $(4)-(3): \implies d = 41$ , $(1): \implies a = 4$ , $(2): \implies c = 26$ , and $(3): \implies b = 4$ . The number of students who opted for Mathematics $a+b+d+15=4+4+41+15=64$ . The number of students who opted for none of the subjects is $f = 120-15-16-9-a-b-c-d = 5$ . The sum of numbers who opted for Mathematics and opted for none of the subjects is $64+5 = \boxed{69}$ .

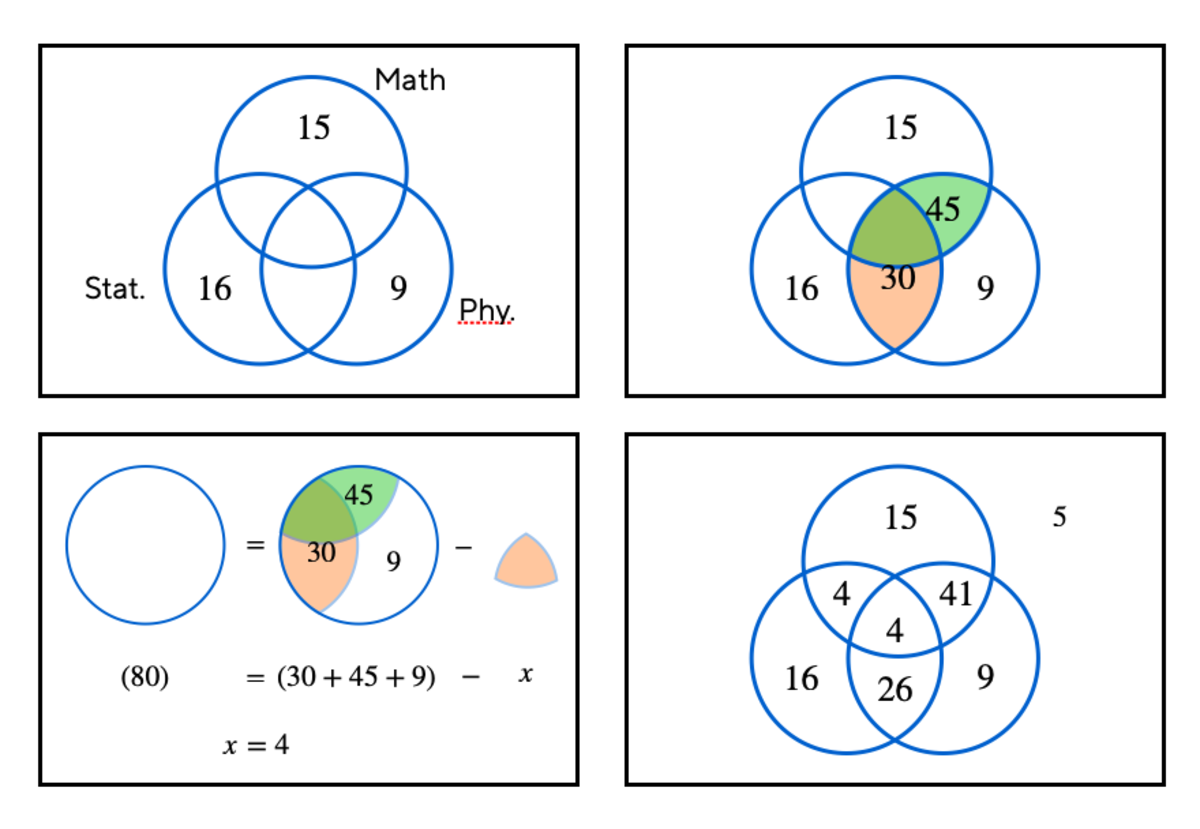
Thus the required answer is

$15 + 4 + 4 + 41 + 5 = \boxed{69}$

Let the number of students who opted for Mathematics, Physics and Statistics be $y$ , for Mathematics and Physics only be $x$ , for Physics and Statistics only be $z$ , for Mathematics and Statistics only be $u$ and for no subject be $n$ . Then

$x+y=45,x+y+z+u+n=120-(15+9+16)=80,x+y+z+9=80\implies u+n=9\implies 15+u+x+y+n=15+45+9=69$ .

Hence the required number is $\boxed {69}$ .