A Pre-RMO question! -12

Label the unknowns as in the Venn diagram above. Then we have:

$\begin{cases} a+ b=8 &...(1) \\ a+ d = 20 &...(2) \\ a+ c = 28 &...(3) \\ a+ c + d = 40 &...(4) \end{cases}$

From $(4)-(3): \implies d = 12$ , $(2): \implies a = 8$ , $(1): \implies b = 0$ , $(3): \implies c = 20$ , and $f = 200-20-36-40-a-b-c-d = 64$ . The sum of numbers who played no game and only played cricket and hockey is $f+d = 64+12 = \boxed{76}$ .

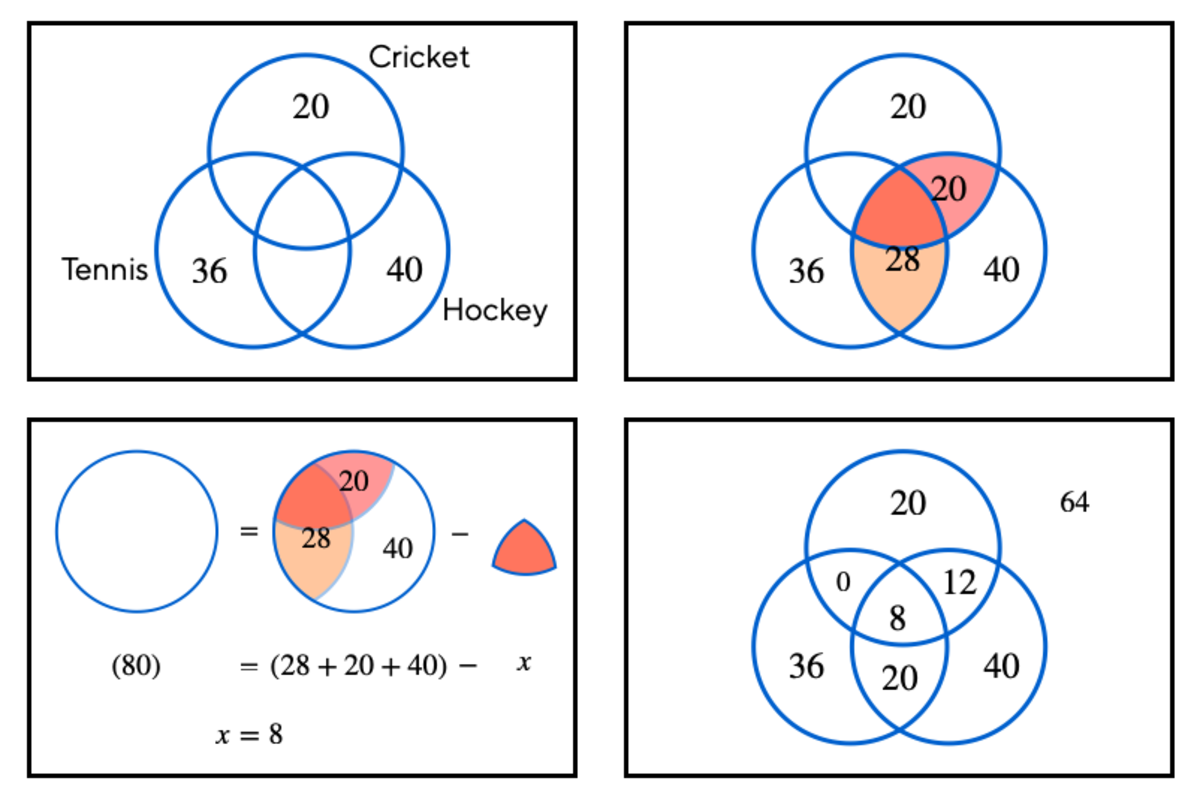
Thus the required answer is

$64 + 12 = \boxed{76}$

Let the number of students who played none of the games be $n$ , played cricket and hockey only be $x$ , played cricket and tennis only be $y$ , played hockey and tennis only be $u$ , and played all the games be $z$ .

Then

$40+20+36+x+y+z+u+n=200$

$\implies x+y+z+u+n=104$ ,

$x+z=20$ ,

$y+z=8$ ,

$u+z=28$ ,

$40+x+z+u=80\implies x+z+u=40$ ,

$y+n=64$ ,

$x-y=12$

$\implies x+n=12+y+n=12+64=76$ .

Hence the required answer is $\boxed {76}$ .