A Pre-RMO question! -26

Let $OX = a$ and $OY = b$

$a^2 + \frac{b^2}{4} = 361$ $\frac{a^2}{4} + b^2 = 484$

Solving, we'll get

$a^2 = 64 \text{ and } b^2 = 420$

$XY = \sqrt{a^2 + b^2}$

$\color{#3D99F6}{\boxed{XY = 26}}$

• We draw the diagram and observe the relations among the two right-angled triangles

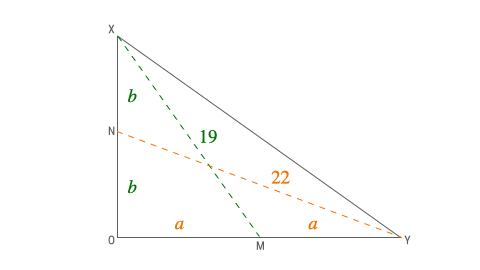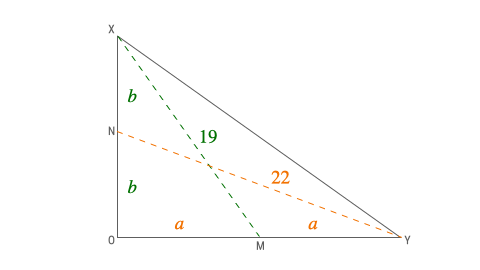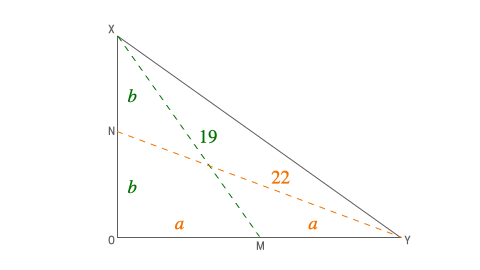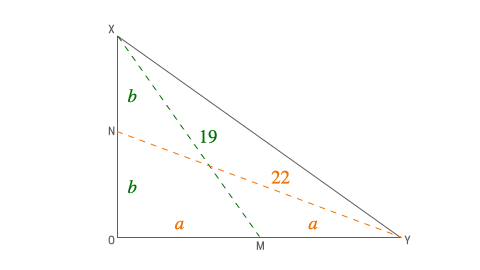
$\begin{cases} (a)^2 + (2b)^2 = (19)^2 &\ldots \blue{(1)} \\ (2a)^2 + (b)^2 = (22)^2 &\ldots \blue{(2)} \end{cases}$

• Add the two equations ${\blue{(1)}} + {\blue{(2)}}$

$\begin{aligned} 5a^2 + 5b^2 &= 845 \\ 5(a^2 + b^2) &= 845 \\ a^2 + b^2 &= 169 &\ldots \blue{(3)} \end{aligned}$

• We find the value of $XY$

$\begin{aligned} XY &= \sqrt{(2a)^2 + (2b)^2} \\ &= \sqrt{4(a^2 + b^2)} \\ &= 2 \sqrt{a^2 + b^2} \\ &= 2 \times \sqrt{\blue{(3)}} \\ &= \boxed{26} \end{aligned}$

Let the position coordinates of $O, X, Y, M, N$ be $(0,0),(a, 0),(0,b),(\frac a2,0),(0,\frac b2)$ respectively. Then

$4a^2+b^2=1444$

$a^2+4b^2=1936$

Solving we get

$a^2=256,b^2=420, a^2+b^2=676$

Therefore $|\overline {XY}|=\sqrt {a^2+b^2}=\sqrt {676}=\boxed {26}$ .

Let length of $\overline{OX}$ be $2x$ and that of $\overline{OY}$ be $2y$ $\implies \overline{XM}=\overline{OM}=x,\overline{ON}=\overline{NY}=y$

In right triangle $\triangle XON$ , $(2x)^2+y^2=(19)^2 \implies 4x^2+y^2=361\cdots (1)$

In right triangle $\triangle YOM$ , $(2y)^2+x^2=(22)^2 \implies 4y^2+x^2=484\cdots (2)$

Adding $(1)$ and $(2)$ ,

$4x^2+y^2+4y^2+x^2=361+484$

$\implies 5y^2+5x^2=845 \implies x^2+y^2=169$

In the big right triangle $\triangle XOY$ ,

$(2x)^2+(2y)^2=(\overline{XY})^2$ $\overline{XY}=\sqrt{4(x^2+y^2)}=\sqrt{4\times 169}=\pm{26} \implies \overline{XY}=26\text{(Since length is positive)}$

$\Large{\boxed{\overline{XY}=26}}$