A Pre-RMO question! -28

Captured Mahdi 's picture.

By symmetry, we know the perpendicular distance from $F$ to $AC =$ perpendicular distance from $F$ to $CE$

Add a line to join $CF$ , the area of the 4 triangles $ABF, BFC, CFD, DFE$ are equal $= A$ ( $\because$ same base 15, and same height )

$3A = \cfrac{30\times15}{2} = 225 \\ \boxed{A = 75}$

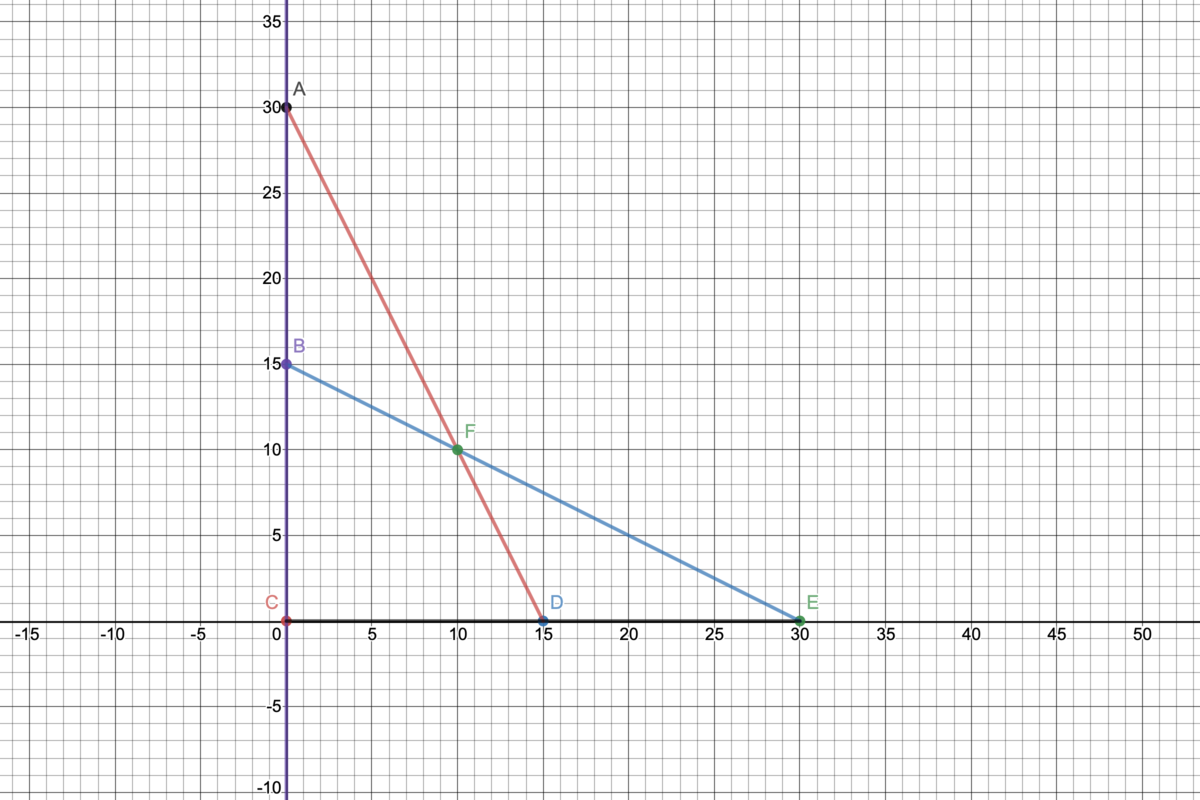
Marking $C$ as the origin for $(0,0)$ , we can determine the coordinates for the other points as shown in the diagram

• The two lines intersect at F, and we can equate the $y$ values

$30 - 2x = 15 - \dfrac{x}{2}$

$x = 10 \implies y = 10$

• Since the height of $\triangle DEF$ is 10, we can find the area

$= \dfrac{1}{2} \times 15 \times 10 = \boxed{75}$

Let the position coordinates of $A, B, C, D, E$ be $(0,30),(0,15),(0,0),(15,0),(30,0)$ respectively. Then equation of $\overline {AD}$ is $y=30-2x$ and of $\overline {BE}$ is

$y=15-\dfrac x2$

Solving these two equations we get the position coordinates of $F$ as $(10,10)$

So, area of $\triangle {DEF}$ is

$x=\dfrac 12\times 15\times 10=\boxed {75}$ .