This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
18 solutions
well,there are only 8 no.s & greatest number is 8 2 = 6 4 , so the answer won't be greater than 5000 , we know answer is not 9 or 12. So only logical choice is 204
How to derive this formula ?
Everybody will think it first (y)
=1^2+2^2+3^2+4^2+5^2+6^2+7^2+8^2 =1+4+9+16+25+36+49+64=204 AND FORMULA Sum= [N(N+1)(2N+1)]/6 N=8 =(8x9x17)/6=4x3x17=204
You are great , dear Sir!
Here, Lower limit of n=1 and Upper limit of n=8 Then,
1^2+2^2+3^2+4^2+5^2+6^2+7^2+8^2 204
sum of squares from 1 to n = n * (n+1) * (2n+1) / 6 here n =8 by substituting n = 8 we get 8 * (8+1 ) * (16+1) / 6 = 8 * 9 * 17 / 6 = 204
n(n+1)(2n+1)/6, sum of squares up to n.
Plugging in 8, we get
8(9)(17)/6=204.
Its better way to use the formula. That is -
1^2 + 2^2 + 3^2 + . . . . . . + n^2 = {n * (n+1) * (2n+1)}/6 ; Where n=8
Took square of each digit from 1 to 8 and added them up.
Ans : 204 sum of squares of 1 to 8 is the answer
that's so easy SUM= n * (n+1) * (2n+1) / 6.
In this question have three question mark ,and options are given in single,two,three,and four digit numbers ,here 204 is only three digit number so i choose that correct one taht's it.
Well My simple logic by seeing multiple choices is 8x8=64 So it's impossible for 12 and 9 Then if 8x8=64, below of 8 (7x7, 6x6), they won't be more than 64 100x8 = 800 < 5463 So it's really impossible too 204 must be true hehe
1+4+9+16+25+36+49+64=204
(1×1)+(2×2)+(3×3)+(4×4)+(5×5)+(6×6)+(7×7)+(8×8) =1+4+9+16+25+36+49+64=204
I did the same as Jithin, wihout any formula, 8² = 64, so... if 64 > 12 & 9, this options were dropped, and only I have 2 options, 5463 & 204, so the ans is 204
1x1+2x2+3x3+4x4+5x5+6x6+7x7+8x8=? ; then
1+4+9+16+25+36+49+64= 204
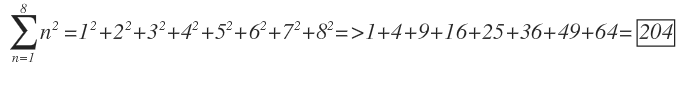
sum of squares from 1 to n = n * (n+1) * (2n+1) / 6
here n =8
by substituting n = 8 we get 8 * (8+1 ) * (16+1) / 6
= 8 * 9 * 17 / 6
= 204 :)