A problem by أحمد الحلاق
Level
pending
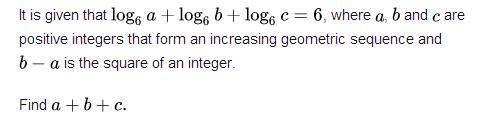
The answer is 111.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We have that lo g 6 a + lo g 6 b + lo g 6 c = lo g 6 ( a b c ) = 6 ⟹ a b c = 6 6 .
Now with r > 1 we have that b = a r , c = a r 2 and a b c = a 3 r 3 = ( a r ) 3 = 6 6 ⟹ a r = 6 2 = 3 6 .
This in turn implies that a c = 6 4 = 2 4 3 4 .
Next, we require that b − a = a r − a = 3 6 − a = n 2 for some (positive) integer n . Since a > 0 we see that n is limited to 1 , 2 , 3 , 4 , 5 , yielding respective values for a of 3 5 , 3 2 , 2 7 , 2 0 , 1 1 . Now as a c = 2 4 3 4 we can only have primes 2 and 3 in the prime factorization of a , and in each case only up to a power of 4 . The only possible value for a among the ones listed above is 2 7 = 3 3 , which yields a value for c of 2 4 ∗ 3 = 4 8 .
Thus a + b + c = 2 7 + 3 6 + 4 8 = 1 1 1 .