A geometry problem by Abhishek Kanigiri

The period of $sinx$ is $2\pi$ , and the period of $sin(nx)$ is equal to $\frac{2\pi}{n}$ .This is because when you plot the graph of $sinx$ we can see that at $2\pi$ the graph repeats.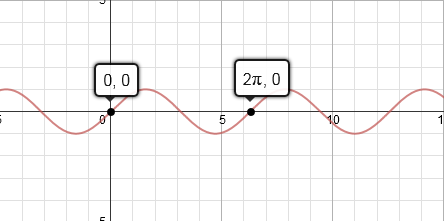

Now when we double the value of $x$ the graph repeats at $pi$ like this ,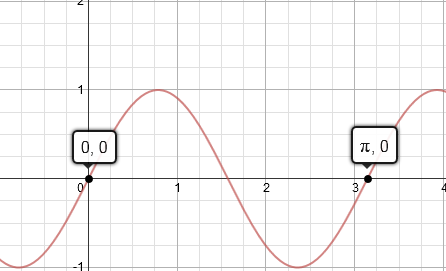

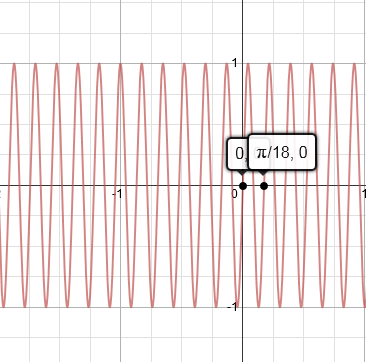
This can be generalized as the period of $sin(n\pi)$ is equal to $\frac{2\pi}{n}$ . Applying it in the question we get the period of $sin(36x)$ as $\frac{2\pi}{36} = \frac{\pi}{18}$ .And this can be checked by plotting the graph.