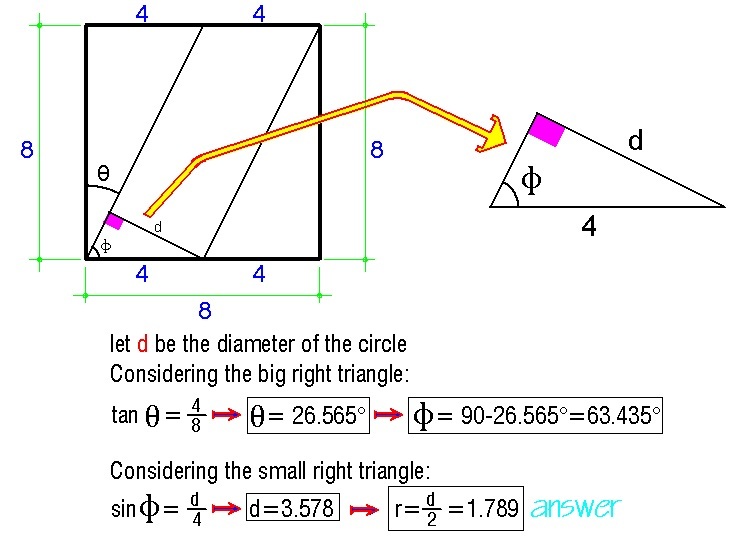
A geometry problem by Ajay Sambhriya

Geometry Level 2

The above shows a square ABCD with side length 8.
M and N are the midpoints of sides AB and CD, respectively.
A circle is inscribed in between lines DM and NB and the bottom side of the square.

Find the radius of this circle to 3 decimal places.


The answer is 1.789.

Ajay Sambhriya by Ajay Sambhriya , 27, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

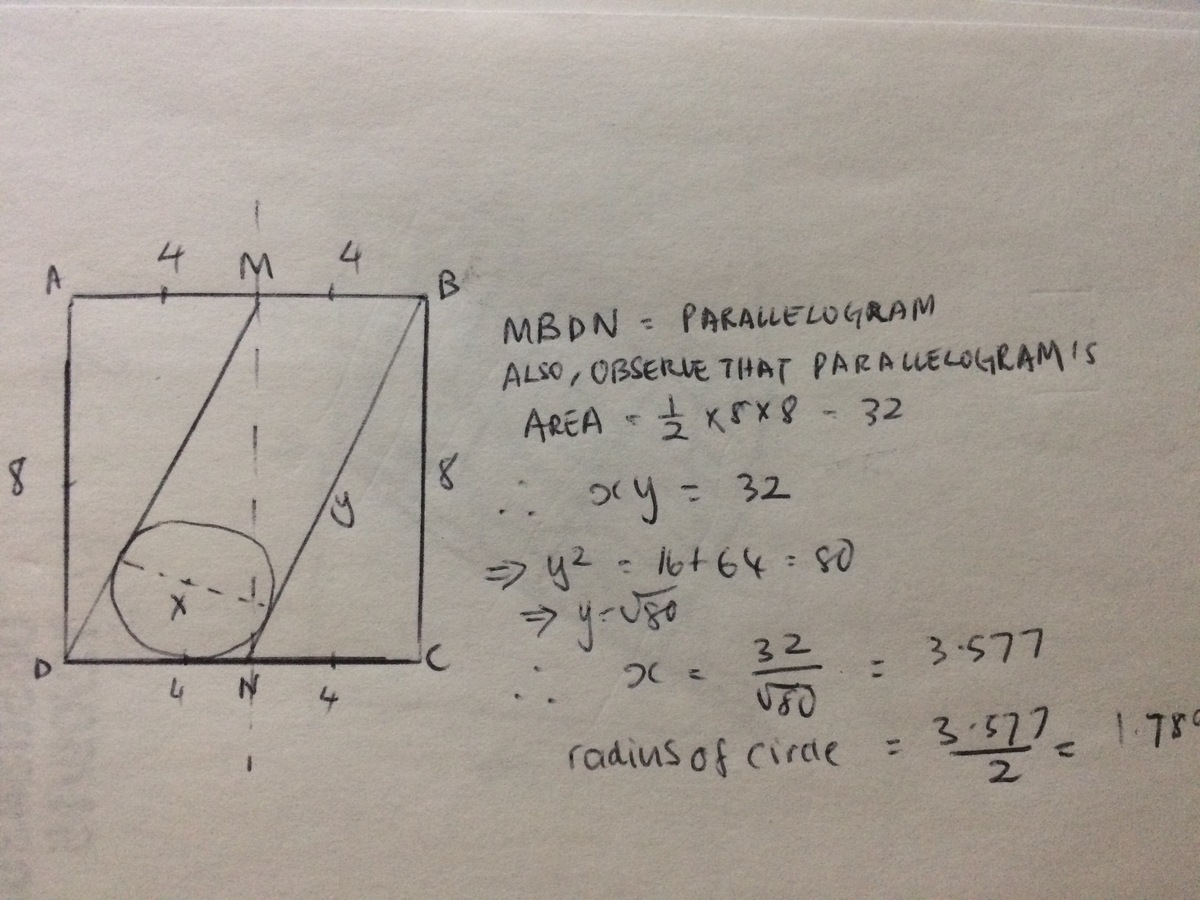
22 Helpful 0 Interesting 0 Brilliant 1 Confused

Great! We can write the area of parallelogram MBND in two different ways: M N × N D MN \times ND and B N × 2 × r BN \times 2\times r . Since they both give us the area of the parallelogram, they must be equal. We already know M N MN , N D ND and we can also find B N BN using the Pythagorean theorem. Using this we get the value of r r .

Pranshu Gaba - 4 years, 3 months ago

Why is that wrong?

AM = 2 AD

angel ADM = 30deg

angel PDN = 60deg

PN / DN = sin 60 = sqrt(3)/2

PN = DN * sqrt(3)/2 = 2 sqrt(3)

r = PN / 2 = sqrt(3) ~ 1.732

عمرو إبراهيم - 4 years, 3 months ago

Log in to reply

Angle ADM is not equal to 30°, that is the reason.

Seyed Seyedy - 3 years, 8 months ago
Ajay Sambhriya
Feb 4, 2017

12 Helpful 0 Interesting 0 Brilliant 0 Confused

Moderator note:

The important observation is that the diameter of the circle is equal to the perpendicular distance between these 2 parallel lines.

Once we realize that, there are many approaches to calculate the distance between these lines.

Right, to show that that the diameter of the circle is equal to the perpendicular distance between the parallel lines, we can use the fact that a tangent to a circle at a point is perpendicular to the radius to that point

Also, it turns out that the condition that circle touches the side CD is redundant. Any circle inscribed between the parallel lines would have the same diameter.

Pranshu Gaba - 4 years, 3 months ago

Why is that wrong?

AM = 2 AD

angel ADM = 30deg

angel PDN = 60deg

PN / DN = sin 60 = sqrt(3)/2

PN = DN * sqrt(3)/2 = 2 sqrt(3)

r = PN / 2 = sqrt(3) ~ 1.732

عمرو إبراهيم - 4 years, 3 months ago

Log in to reply

Actually, angle ADM is tan ⁡ − 1 1 2 = 26.6 \tan^{-1} \frac{1}{2} = 26.6 degree and not 30 degrees.

Pranshu Gaba - 4 years, 3 months ago

Even though there are many other ways to solve this problem, This one is the best. thanks for sharing your perspective.

Mehran Ali Ansari - 3 years ago

8 Helpful 1 Interesting 1 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...