A geometry problem by Ajay Sambhriya

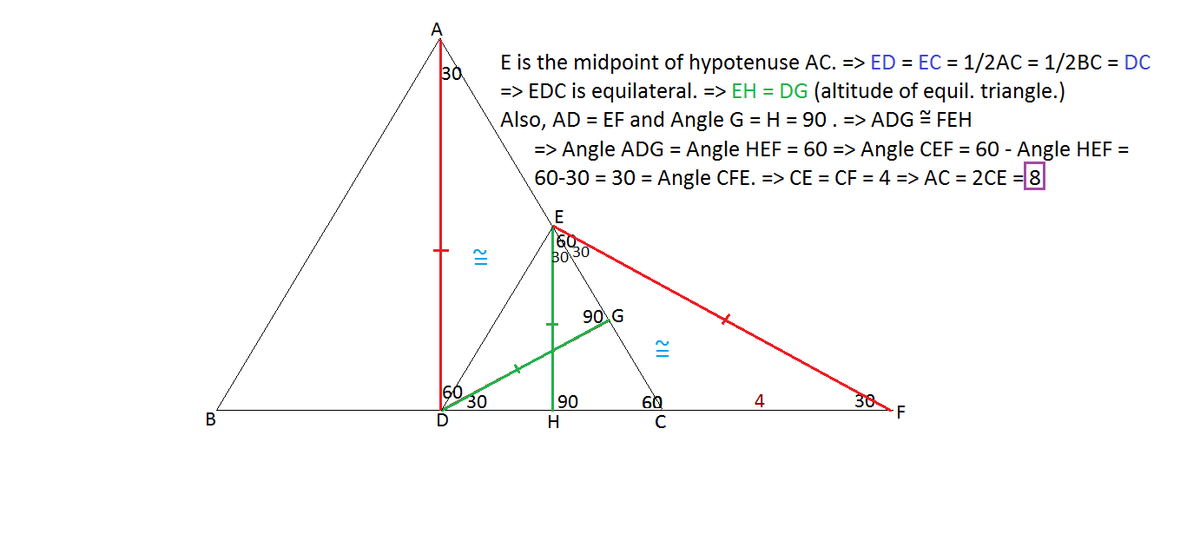
The above shows an equilateral triangle A B C with C L as its altitude.
Given that E D = C L , C E = E B , B D = 4 , find the side length of this equilateral triangle A B C .
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Do u urself frame all these stuffs?
If AL = x ,
C L = E D = 3 x
∠ E B D = 1 2 0 ∘
Apply L a w o f C o s i n e s on △ E B D
x 2 − 2 x − 8 = 0
⟹ x = 4 , − 2
As a side length( x ) cannot be negative, x = 4 ⟹ A B = 2 x = 2 ⋅ 4 = 8
Let each side of Triangle ABC be 'a'
CL = ED = √3a/2 , CE = EB = a/2
Angle EBD = 120°
Applying sine rule , ED / sin120 = EB / sin EDB
Solving for Angle EDB , we get Angle EDB = 30° = Angle BED
Therefore , EB = BD
a/2=4 Therefore ,
a=8
Let CE = EB = x
Since it is equilateral, BL = x and CL = x*sqrt(3)
So ED = x*sqrt(3)
By Law of Cosines (x sqrt(3))^2 = x^2 +4^2 - 2 4 x cos120
3x^2 = x^2 +16 +4*x
2x^2 - 4*x - 16 = 0
x^2 - 2*x - 8 = 0
(x-4)*(x+2) = 0
x = 4 or -2 discard negative value
x = 4 so CB = 2*x = 2 times 4 = 8