A problem by Ajay Sambhriya
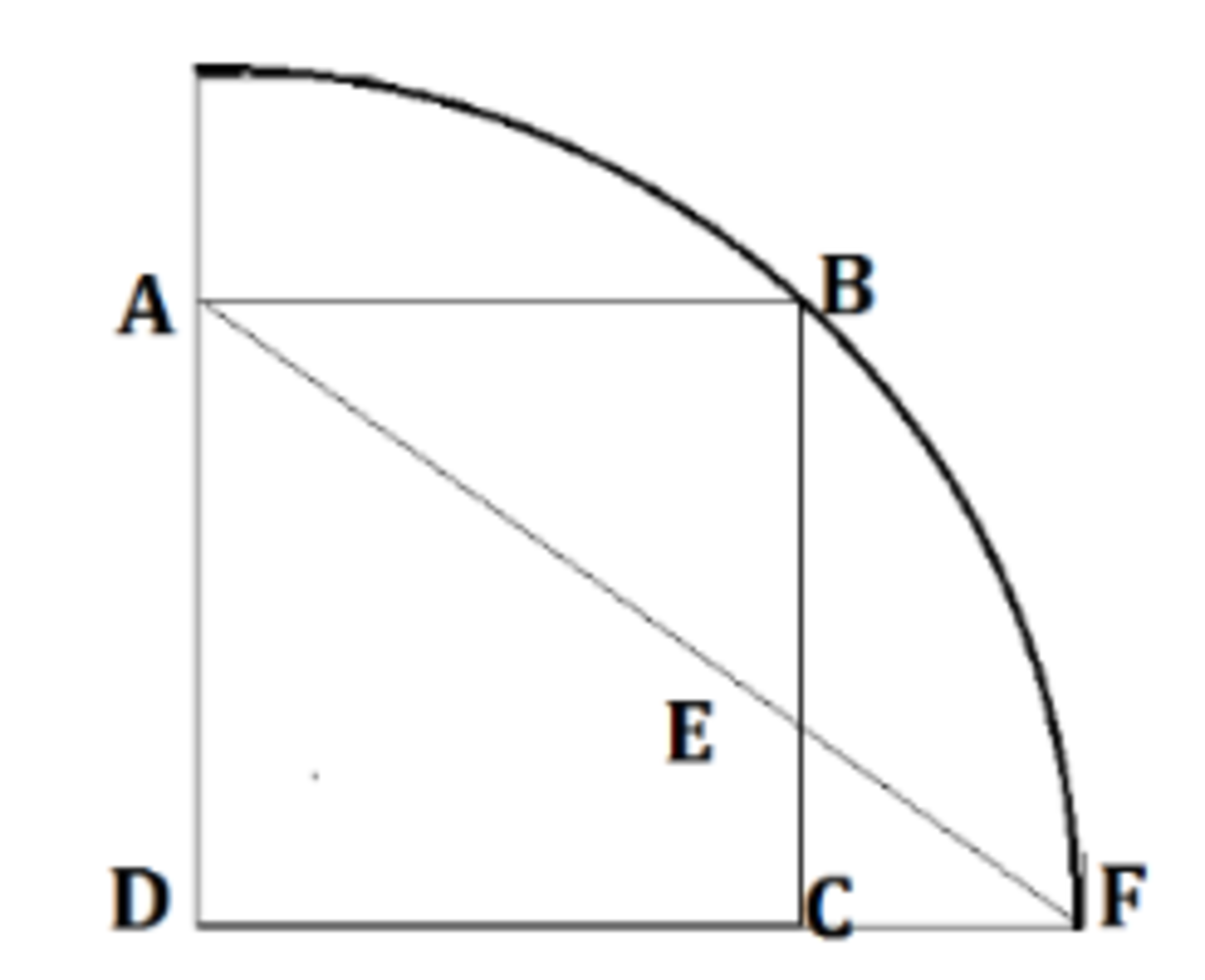
A square is inscribed in a quarter circle as shown above.
Given that AF meets CB at E, and the radius of this quarter circle is 12. Find the length of AE to 2 decimal places.
The answer is 10.39.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
DB is a radius and so = 12. It is also the diagonal of the square ABCD, which means each side of the square is 6*sqrt(2). We can coordinize the problem. Let D be the origin. D = (0,0(. F = (12,0) A =(0,6sqrt(2) The equation of the line AF is y = (-sqrt(2)/2)x + 6sqrt(2). The equation of the line CB is x = 6sqrt(2). The intersection is the coordinates of E. E = (6sqrt(2), -6 + 6sqrt(2). The distance AE is given by sqrt((6sqrt(2) - 0)^2 + (-6 + 6sqrt(2) -6sqrt(2))^2) = sqrt(72 + 36) = sqrt(108) = 6sqrt(3) = 10.392. Ed Gray