A geometry problem by Ajay Sambhriya
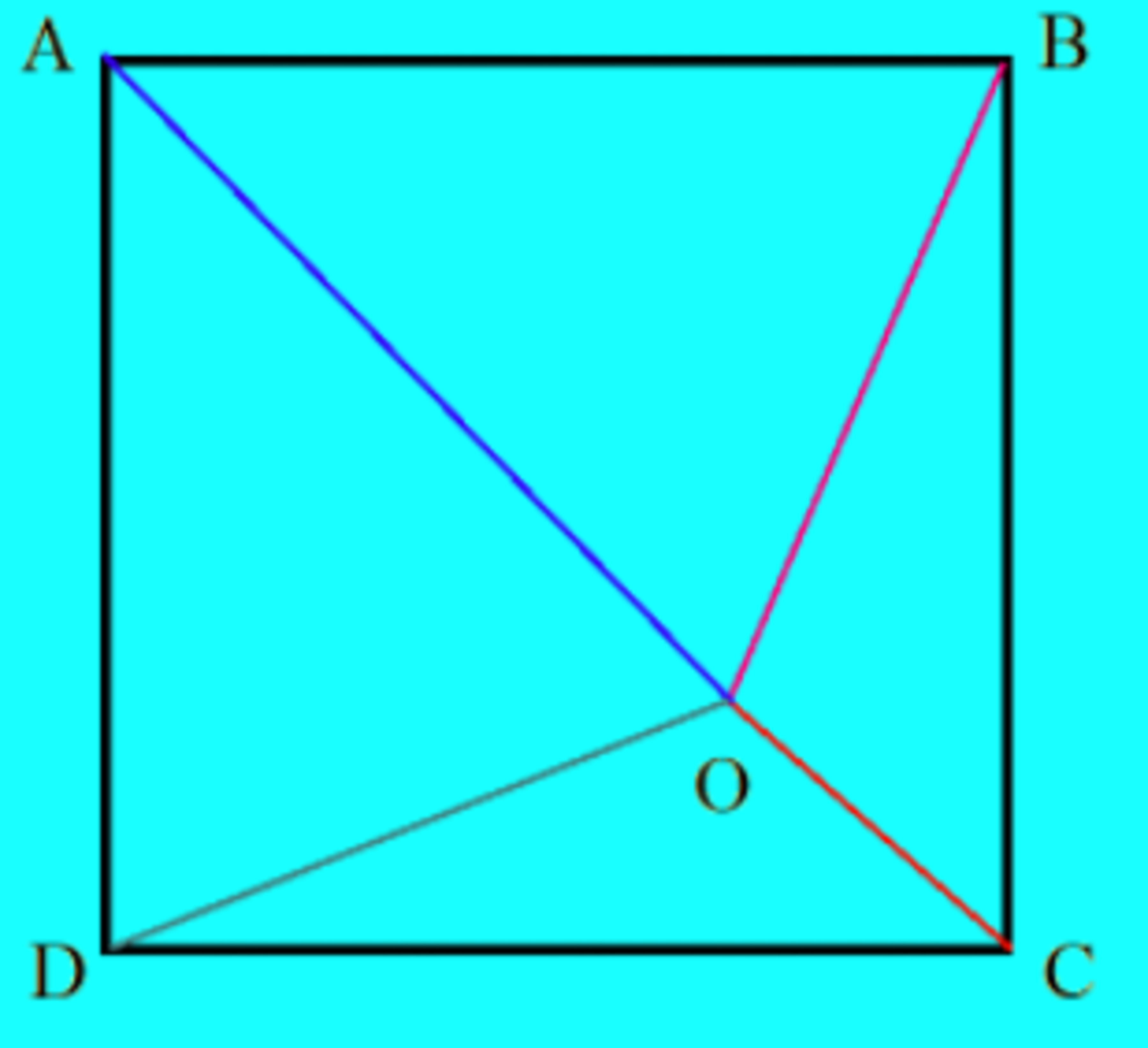
The figure shows a square A B C D with side length 5.
O is a point inside this square such that D O = O B and A O = 3 ⋅ O C .
Find the sum of area of triangles A O B and D O C .
The answer is 12.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
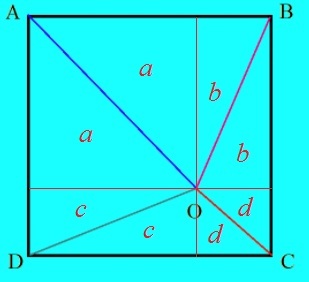
Draw two perpendicular lines each parallel to the sides of the square through O . The two lines divide the square into 4 pairs of equal area triangles a , b , c and d . Implying that the area of the square [ A B C D ] = 2 ( a + b + c + d ) = 5 2 = 2 5 .
We note that [ A O B ] + [ D O C ] = a + b + c + d = 2 2 5 = 1 2 . 5 .
Nice solution sir
What software do you use, to create solutions?
Log in to reply
AutoCAD software
AutoCAD is used across a wide range of industries, by architects, project managers, engineers, graphic designers, and many other professionals.
Thanks sir 😁
Draw a line through point O parallel to AD. Let the intersection of this line and AB be denoted F, and define FO = h. Then OG = 5 - h, where G is the extension of FO until it intersects CD. Then the sum of areas is (1/2)(5)(h) + (1/2)(5 -h)(5) = 12.5. Ed Gray
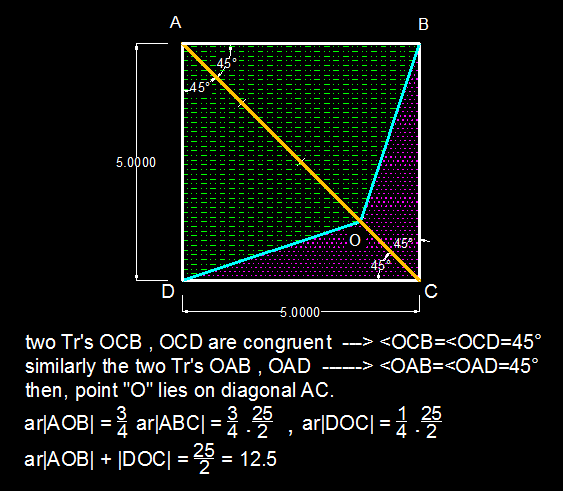
A C = A O + O C but A O = 3 ( O C ) . Therefore, A C = 3 ( O C ) + O C = 4 ( O C ) . We find O C = 4 5 2 . It follows that A O = 3 ( 4 5 2 ) = 4 1 5 2 .
A A O B = 2 1 ( 5 ) ( 4 1 5 2 ) ( sin 4 5 ) = 9 . 3 7 5
A D O C = 2 1 ( 5 ) ( 4 5 2 ) ( sin 4 5 ) = 3 . 1 2 5
Finally,
A A O B + A D O C = 9 . 3 7 5 + 3 . 1 2 5 = 1 2 . 5