Slanted tiles
The above shows a square A B C D with side length 6.
M , N , O , P are points on the sides A D , B A , C B , D C , respectively such that A M = D P = C O = B N = 2 .
Find the area of the green square.
The answer is 14.4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
I like these kind of problems because all the ways you can look at it. Congruence works but for example placing an x and an y axis works too.
Log in to reply
yes me too....many ways to solve them :) but Similarity Rocks
Log in to reply
Yeah I used similarity too, but wanted to find other ways too. Didn't write them out though
How <BHC = <OIC = <ODC ???
Let X = intersection of AP and BM.
Then AMB is similar to XAB.
The diagonal MB is 4 0 (using Pythagorean theorem), and the diagonal AB is obviously 6. Thus the ratio between lengths of AMB and XAB is 4 0 : 6 , and the areas have the ratio 4 0 : 3 6 = 1 0 : 9 .
Since the area of AMB is 6, the area of XAB is 6 × 9 / 1 0 or 5.4.
The white part of the square is the union of four disjoint triangles congruent to XAB, so the white area is 4 × 5 . 4 = 2 1 . 6 .
Finally, the green area is 6 2 − 2 1 . 6 = 1 4 . 4 .
Referring to Ajay's figure, consider dividing the the whole figure into 9 equal sized subsquares:
- The central subsquare is entirely green and has area 4
- The green parts of the top-middle and bottom-middle subsquares fit together to make a square of area 4
- The green parts of the left-middle and right-middle subsquares fit together to make a square of area 4
- The green parts of the 4 corner subsquares fit together to form a figure which is similar to the complement of the entire original figure (i.e., a green square with a tilted white subsquare)
If the area of the original green square is A, then A therefore satisfies:
A = 4 + 4 + 4 + 4 3 6 3 6 − A ⇒ A = 1 6 × 1 0 9 = 1 4 . 4
I solved this originally using similarity, but the jigsaw puzzle solution doesn't even require square roots...
We are told that the green area is a square, so all of its angles are right angles.
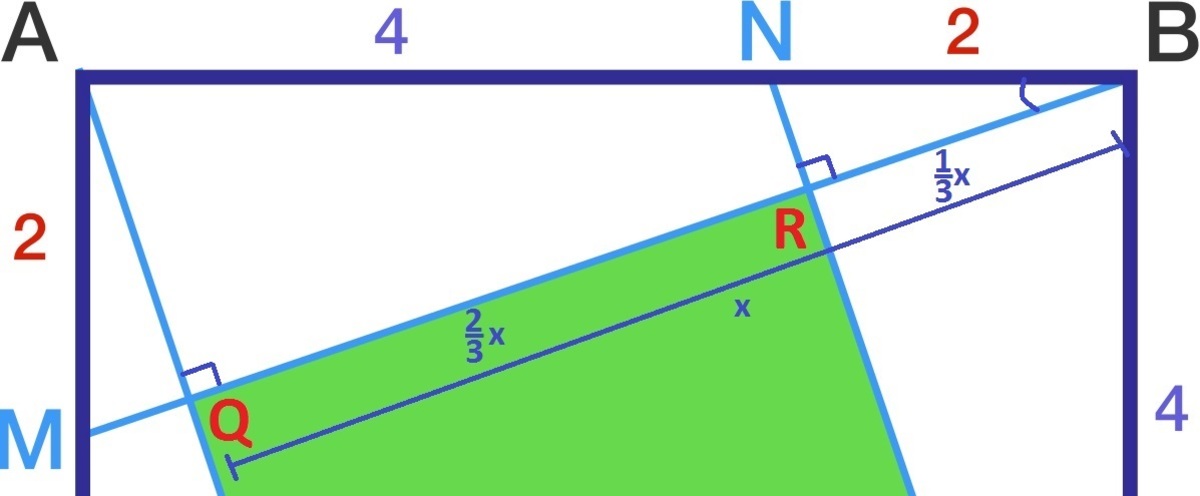
⇒ m ∠ A Q B = m ∠ N R B = 9 0 ∘
∠ B ≅ ∠ B
⇒ A A : △ A Q B ∼ △ N R B
Q B = x 6 2 = x R B ⇒ R B = 3 1 x ⇒ Q R = 3 2 x
All of this is also correspondingly happening to
△
A
D
P
.
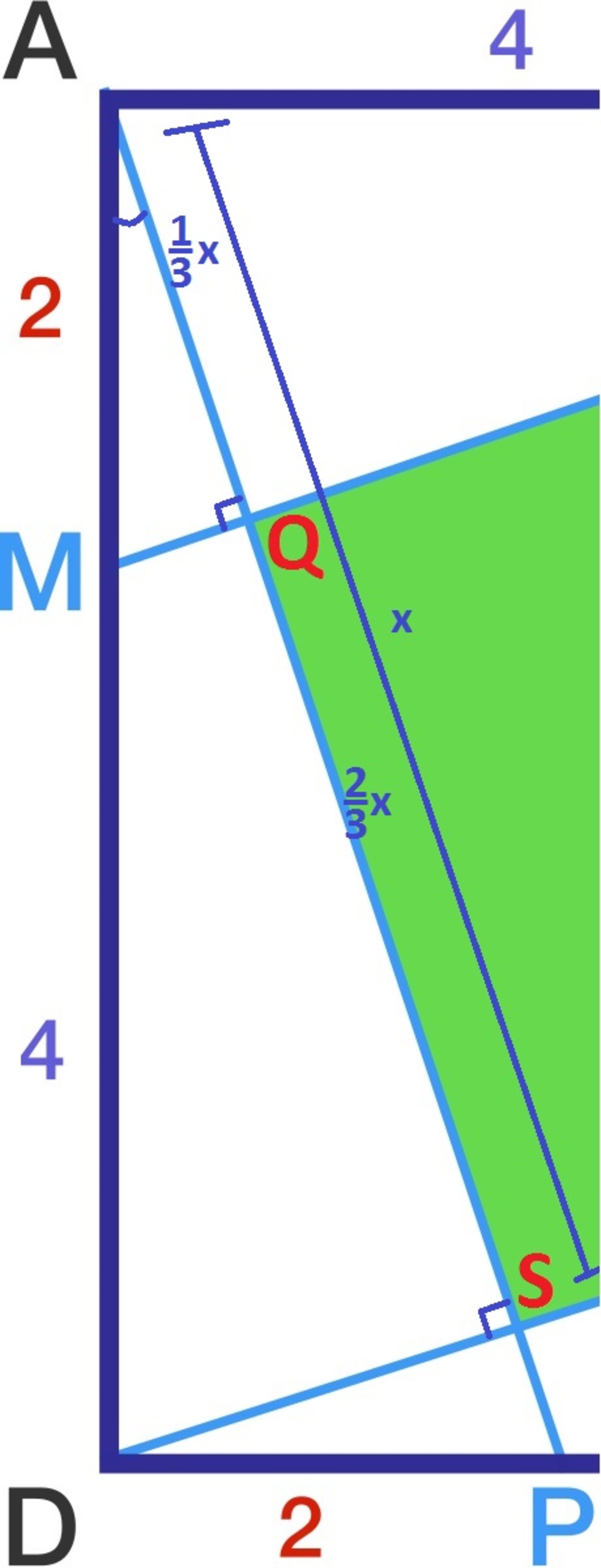
S A S : △ A B M ≅ △ D A P ⇒ ∠ A B M ≅ ∠ D A P
A A S : △ A Q B ≅ △ D S A ⇒ Q B = S A = x ∴ A Q = 3 1 x
△ A Q B Pythagorean Theorm ( 3 1 x ) 2 + x 2 = 6 2 9 1 x 2 + x 2 = 3 6 9 1 0 x 2 = 3 6 9 1 0 x 2 = 3 6 Note: x > 0 , so x 2 only has one solution. 3 1 0 x = 6 x = 1 0 1 8 3 2 x = 1 0 1 2 = s i d e o f t h e G r e e n S q u a r e A G r e e n S q u a r e = ( 1 0 1 2 ) 2 = 1 0 1 4 4 = 1 4 . 4 □
Since the slope is 1:3, the sides of the smaller triangle are x, 3x and (root 10)x.
The side of the green square = 6x.
As (root 10)x = 2, x^2 = 4/10.
Area of green square = 36x^2
= 36 × 4 /10 = 144 /10 = 14.4.
The area of ABCD is 36.
The area of two of the big right triangles is 12.
With that in mind, the area of the remaining parallelogram BODM is 24.
The width of the base of BODM is equal to the hypotenuse of one of the big triangles.
- B 2 = 2 2 + 6 2
- B 2 = 4+36
- B 2 = 40
- B = 4 0
X
- A = B × h
- h = B A
- h = 4 0 2 4
- h = 1 0 1 2
The side length of the green square is equal to h.
- h 2 = 1 0 1 4 4
- 1 4 . 4
let
A = area of the green square
S = area of the big square
T = area of one big triangle
t = area of one small triangle
A = S − 4 T + 4 t (working formula)
Area of the small triangle:
let angle DAP = ɸ
so, tan ɸ = 6 2 = 3 1 , from here we compute for the hypotenuse and that is 1 0 .
considering one small triangle,
let y be the side opposite angle ɸ and x be the side adjacent to angle ɸ
by similar figures we have,
1 y = 1 0 2
y = 1 0 2
by similar figures again,
3 x = 1 0 2
x = 1 0 6
Solving the area of one small triangle, we have
t = 0 . 5 ( 1 0 2 ) ( 1 0 6 ) = 0 . 6
Now we solve the area of the green square,
A = S − 4 T + 4 t
A = 6 2 − 4 ( 2 1 ) ( 2 ) ( 6 ) + 4 ( 0 . 6 ) = 1 4 . 4
Note that we added the area of the 4 small triangles because it was subtracted twice.
Let H denote the intersection points of the straight lines B M and N C ,
let I denote the intersection points of the straight lines D O and N C , and
let J denote the intersection points of the straight lines D O and A p .
Since the triangles D O C and B H C are the same, and because M B ∥ D O , then ∠ B H C = ∠ O I C = ∠ O D C .
Thus, the triangle O D C is similar to the triangle O I C .
We can have O C O D = O I O C . By Pythagorean theorem , O D = ( D C ) 2 + ( O C ) 2 = 6 2 + 2 2 = 2 1 0 . Upon subsitution, we get O I = 1 0 6 .
Now the side length of the square is s : = O D − D J − I O = 2 1 0 − I C − 1 0 2 = 2 1 0 − 1 0 6 − 1 0 2 = 1 0 1 2 .
And our answer is s 2 = 1 4 . 4 .