This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
The given image is a 2×2 grid with small 2×2 grid at the middle. To get the no. of squares in a 2×2 grid, add the sum of the squares of 1 and 2 i.e 1^2 + 2^2 = 1+ 4= 5 Since there is another 2×2 grid at the middle multiply 5 by 2 Therefore, there are 10 squares.
Another solution 2(1^2 + 2^2) = 2(5) =10 squares
One big + one small + 4 square parts of the big square & 4 square parts in the small square.
4 yellow & green squares + 4 small green squares + 1 big green square + 1 biggest yellow & green square
Bonus question: How many quadrilaterals are in the image
18 quadrilaterals Two lines are dividing yellow square in two rectangles each, so there are 4 yellow rectangles. Same with green square. There are 10 squares and 2*4 rectangles, so in total 18 quadrilaterals.
The large square The green central square The four squares into which the green square is divided. The four squares into which the large square is divided 4+4+1+1 = 10
The given image is a 2×2 grid with small 2×2 grid at the middle. To get the no. of squares in a 2×2 grid, add the sum of the squares of 1 and 2 i.e 1^2 + 2^2 = 1+ 4= 5 Since there is another 2×2 grid at the middle multiply 5 by 2 Therefore, there are 10 squares.
Another solution 2(1^2 + 2^2) = 2(5) =10 squares
The whole square, the whole green square , and the divided yellow and green square..
5 of the green ones ( 4 inner, 1 whole )and 5 of the brown ones( 4 inner, 1 whole)
count the lines. they add up to 10.
The 8 directly visible, as well as the square as a whole and the green square formed by the 4 small squares. 10.
Inside as well out side will have 5 each ,so total 10 Ans K.K.GARG,India
Answer by Krishna
1 exterior,4pieces of the outer one,1inner and 4 pieces of the inner one
1 big square divided into 4 smaller squares making a total of 5. 1 central smaller square divided into 4 even smaller ones making another total of 5. Together they make 10.
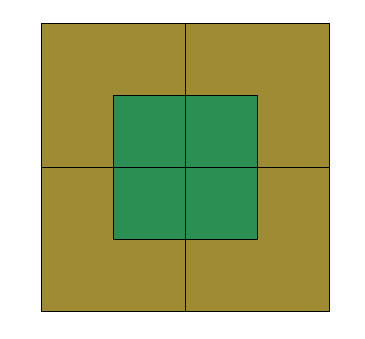
There's the largest square: 1.
There's the green square: 1.
The green square splits into 4 green squares: 4.
There's 4 squares: top left, top right, bottom left, bottom right.
So there's a total of 1 + 1 + 4 + 4 = 1 0 squares.