E field!

Electricity and Magnetism Level 2

A spherical shell of uniform charge density σ has a circular hole cut out of it as shown below:

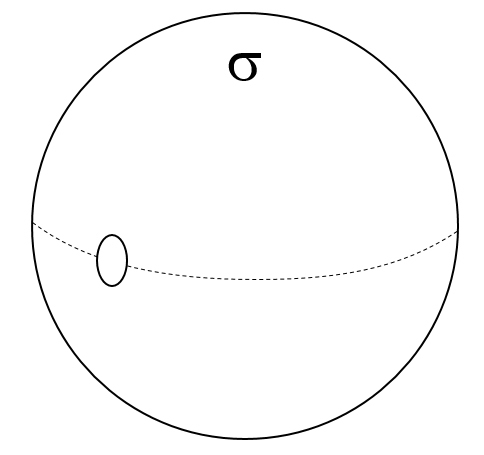
What is the Electric Field at a radius just outside the sphere, directly over the center of the circular, cut-out hole?

HINT: the hole is small enough that you can treat it as flat, and the point at which you are calculating the field is so close to the hole that it can be approximated as an infinite plane.

σ/ϵo σ/2ϵo 3σ/2ϵo Fσ/4ϵo 2σ/ϵo Fσ/ϵo 7σ/2ϵo

1 solution

Steven Chase
Oct 8, 2017

We can treat this problem as a superposition of the field due to a spherical charge sheet (positive), and a flat charge sheet (negative). Use Gauss's Law twice.

For the positive sphere:

$E \, S = \frac{q_{enc}}{\epsilon_0} \\ E \, 4 \pi R^2 = \frac{4 \pi R^2 \sigma}{\epsilon_0} \\ E = \frac{\sigma}{\epsilon_0}$

For the negative plane with infinitesimal area $A$ :

$E \, S = \frac{q_{enc}}{\epsilon_0} \\ E \, 2 {A} = \frac{-\sigma \, {A}}{\epsilon_0} \\ E = -\frac{\sigma}{2 \epsilon_0}$

The superposition of the two fields is therefore:

$E_{total} = \frac{\sigma}{\epsilon_0} -\frac{\sigma}{2 \epsilon_0} = \frac{\sigma}{2 \epsilon_0}$

E field!

1 solution

0 pending reports