A pulley on a pulley

Classical Mechanics Level 4

The Image below shows two pulleys, the higher of which is fixed in place. The other pulley is attached to the $6\text{ kg}$ mass by a string running over the first pulley. The pulleys turn without friction. With what acceleration, and in what direction, will the $2\text{ kg}$ mass begin to move?

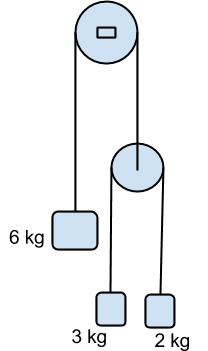
Assumptions String and pulleys themselves are all massless

\frac{g}{9} downwards

\frac{g}{9} upwards

\frac{g}{3} upwards

\frac{2g}{9} upwards

1 solution

Andrew Normand
Jan 20, 2017

I solved this problem by equating the tension in each rope to the force on each block, which is equal to its weight plus its acceleration. I called T1 the tension in the string attached to the 6kg mass, and T2 the tension in the other string. I called a1 the anticlockwise acceleration of the T1 string and a2 the anticlockwise acceleration of the other string. Doing this gave me the following 4 equations:

$T1 = 6(g - a1)$ - Weight minus downwards acceleration for the 6kg block

$T2 = 2(g + a1 + a2)$ Weight plus upwards acceleration for 2kg block

$T2 = 3(g +a1 - a2)$ Weight plus acceleration for 3kg block

$T1 = 2T2$ The two T2 strings must have the same combined tension as T1.

Solving these equations you should find that a1 is g/9 and a2 is 2g/9, so the total acceleration of the 2kg block is 3g/9 = g/3

A pulley on a pulley

1 solution

0 pending reports