A geometry problem by A Former Brilliant Member

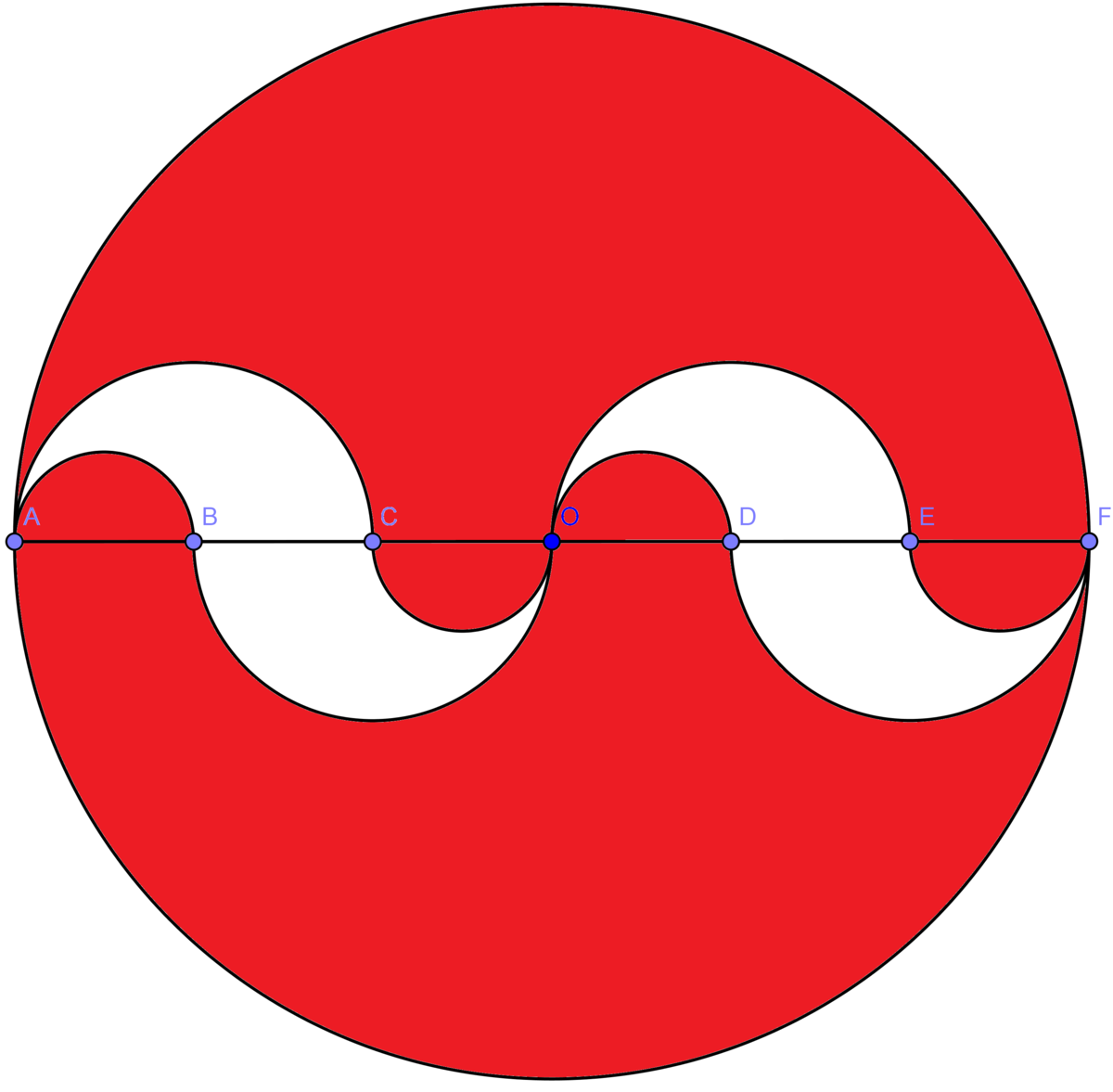
First, let's discover the area of the big circle, that have radius 6. ${\pi{R}^{2}} = {36\pi}$ , that is the area we want.

If $OF = 6$ , $OD = DE = EF = 2cm$ , because we have 3 equal segments that makes $6cm$ together.

We have the semi-circle with radius $DE = 2cm$ and a semi-circle with radius ${{OD} \over {2}} = {1 cm}$ . So, we can get the area of one part of the total white area:

${{\pi{2}^{2}} \over {2}} - {{\pi} \over {2}}$

${2\pi} - {{\pi} \over {2}}$

We have 4 parts of the white above, so the red area is:

${36\pi} - {{4} \times ({2\pi} - {{\pi} \over {2}})} =$

${36\pi} - {({8\pi} - {{4\pi} \over {2}})} =$

${36\pi} - {6\pi} =$

$30\pi {cm}^{2}$ .