A geometry problem
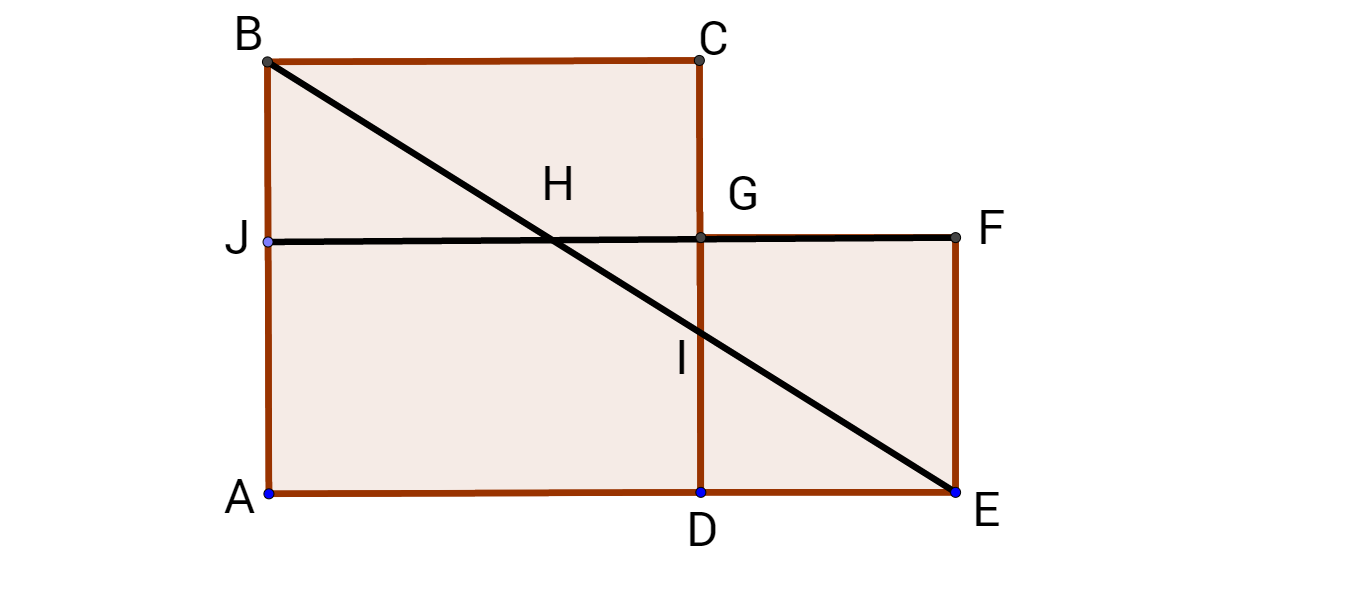
In the figure above, A B C D is a square and A E F J is a rectangle. If J B = I D and A B = 1 1 1 . Find the area of the rectangle A E F J .
The answer is 12321.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
How do you simplify line 5 to get AE=...
Did the exact same
The problem gives away the answer without requiring proof by simply using JB=0
That's a clever trick! If J coincides with B , then all the conditions are satisfied, and rectangle A E F J is congruent to the square A B C D . However, note that the area of the rectangle is equal to the area of the square, even if J B = 0 . Alan has proved it in his solution.
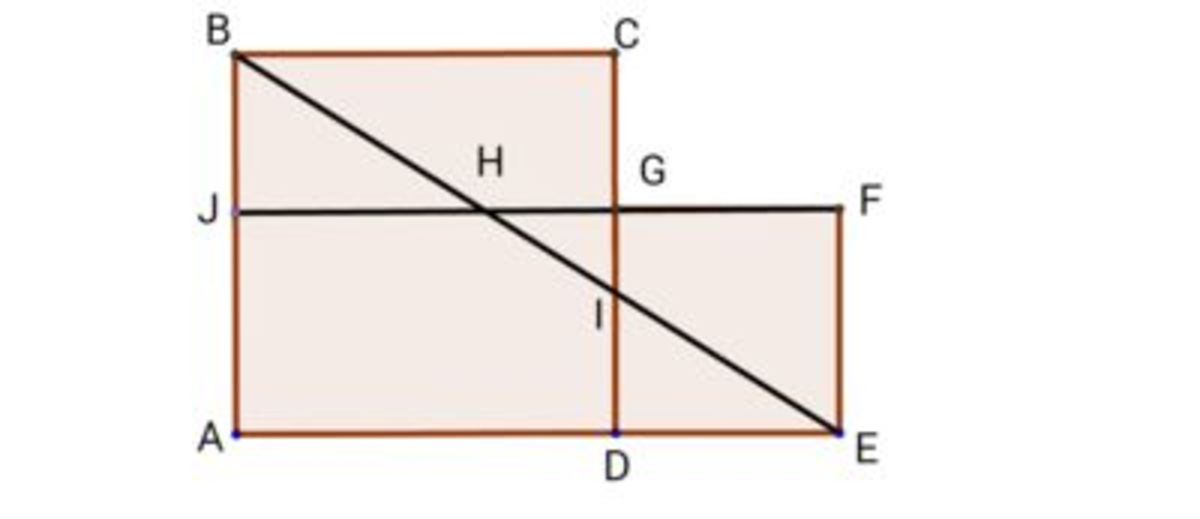
Given: J B = I D , A B = 1 1 1 , Let [ A E F J ] denote the area of rectangle A E F J .
Solution: In △ J B H & △ D I E ,
∠ J B H = ∠ D I E [Corresponding angles]
∠ B J H = ∠ I D E [corresponding angles]
JB = ID [Given]
⇒ △ J B H ≅ △ D I E [SAS congruence]
⇒ [ J B H ] = [ D I E ] .......(1)
Similarly, in △ B C I & △ H F E
∠ C B I = ∠ F H I [Corresponding angles]
F E = I G + I D = I G + J B = I G + C G = C I i . e . , F E = C I
∠ B C I = ∠ F H I [Angles of square & rectangle]
⇒ △ B C I ≅ △ H F E
⇒ [ B C I ] = [ H F E ] .......(2)
[ A E F J ] = [ A J H I D ] + [ I D E ] + [ H F E ]
= [ A J H I D ] + [ J B H ] + [ B C I ] ...........From (1) & (2)
= [ A B C D ] = A B 2 = 1 1 1 2 = 12321
This is the construction for drawing a rectangle given one side and having the area of a given square.
I think the diagram should be redrawn as it doesn't match the sizes and proportions.
Let A B = x and J B = I D = a . Then D E = A E − x and A J = E F = x − a . △ E D I and △ E A B are similar, so I D D E = A B A E ⟹ a A E − x = x A E ⟹ A E = x − a x 2 . Finally, [ A E F J ] = A E ⋅ A J = x − a x 2 ⋅ ( x − a ) = x 2 . So, the answer is 1 1 1 2 = 1 2 3 2 1 .