A Windy Day on Mars
Given that the maximum wind speed measured on Mars is approximately 60 miles per hour (mph), find an approximation to the corresponding wind speed on Earth, at standard sea level pressure, which would give rise to the same pressure on a surface perpendicular to the wind direction.
A typical density of air on Mars is 0.0163 times the density of air at standard temperature and pressure at sea level on Earth.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
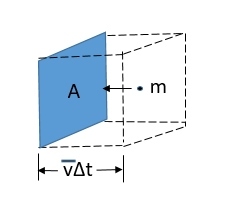


Imagine a tube of fluid (liquid or air) of density ρ is moving at a speed of v towards a wall. The cross section of the tube is A as shown below.
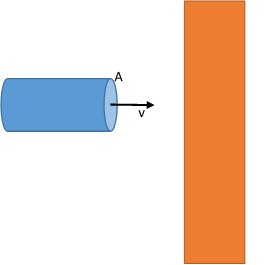
The volume of fluid that hits the wall in time dt will be, d V = A v d t
The momentum of the fluid that hits the wall in time dt is ρ ( A v d t ) v
If the fluid stops and then falls freely just after hitting the wall, then the change in momentum in time dt will be d p = ρ ( A v d t ) v
(Note: For gasses, the collision is nearly perfectly elastic, resulting in twice the impulse due to Newton's third law. d p = 2 ρ ( A v d t ) v )
Force on the wall F = d t d p = ρ A v 2
Pressure generated on the wall will be
P = A F = ρ v 2
Density of air is different on the Mars and the Earth, therefore, for the same pressure on the wall
ρ Earth v Earth 2 = ρ Mars v Mars 2
Plugging in the values, we get,
v E a r t h = 7 . 7 mph .