Have Chocolate, Will Travel

Algebra Level 3

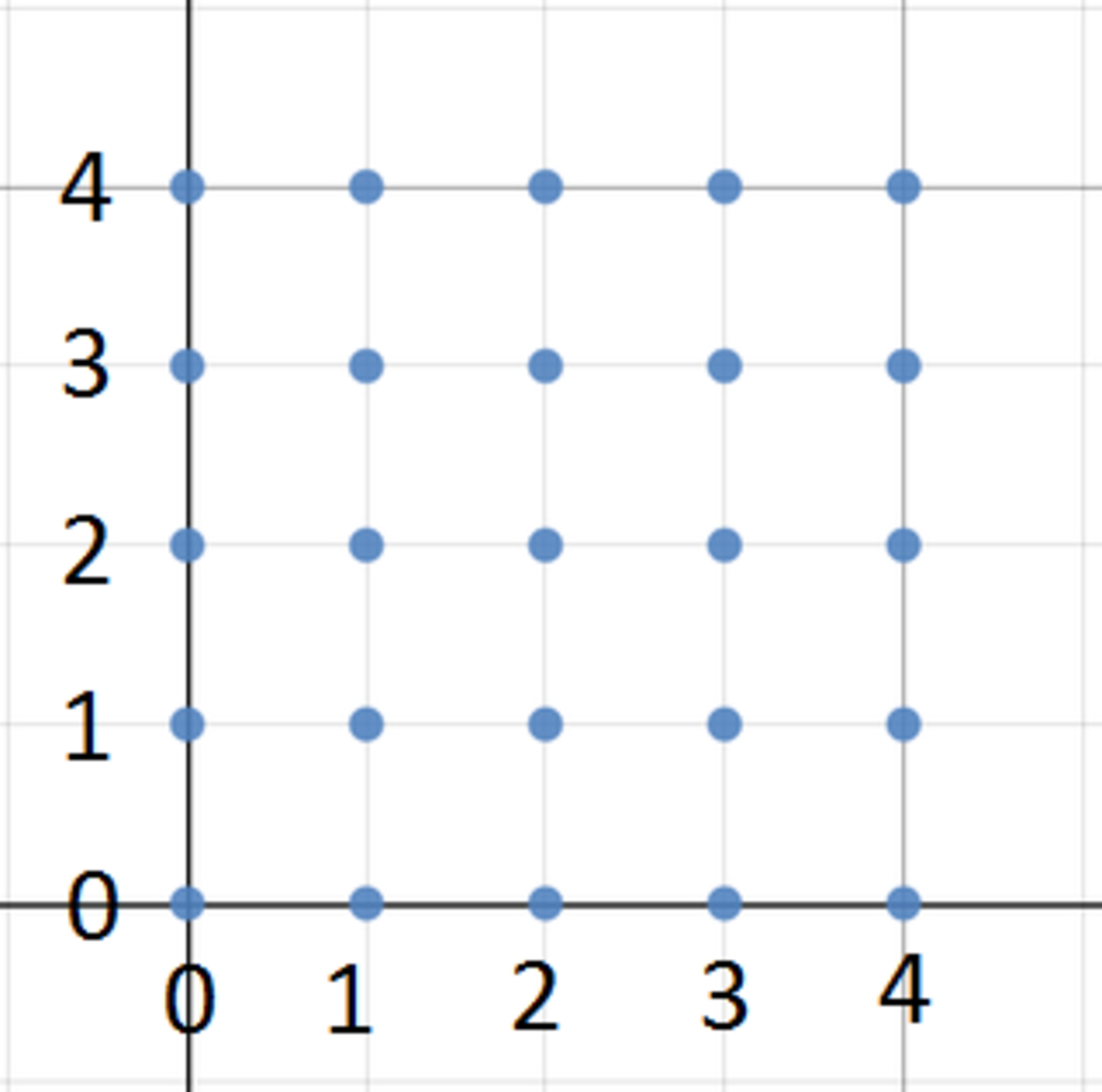
A traveler visits each point ( x , y ) (x,y) with integer coordinates where 0 ≤ x , y ≤ 4 0\leq x,y \leq 4 (each blue dot in the picture). At each of these points ( x , y ) (x, y) , the traveler eats 1 2 max ⁡ { x , y } + 1 \frac {1}{2\max\{x,y\} + 1}

chocolate bar(s). How many chocolate bars will the traveler eat in all?

Notation . max ⁡ { x , y } \max\{x,y\} represents the largest value in the set { x , y } \{x,y\} .


The answer is 5.

Damon Demas by Damon Demas

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Let's go coordinate wise! ( 0 , 0 ) → 1 (0,0) → 1

( 0 , 1 ) , ( 1 , 0 ) , ( 1 , 1 ) → 3 × 1 3 (0,1) , (1,0), (1,1)→ 3\times\frac{1}{3}

( 2 , 0 ) , ( 2 , 1 ) , ( 0 , 2 ) , ( 1 , 2 ) , ( 2 , 2 ) → 5 × 1 5 (2,0), (2,1), (0,2),(1,2), (2,2) → 5\times\frac{1}{5}

( 3 , 0 ) , ( 3 , 1 ) , ( 3 , 2 ) , ( 0 , 3 ) , ( 1 , 3 ) , ( 2 , 3 ) , ( 3 , 3 ) → 7 × 1 7 (3,0),(3,1),(3,2),(0,3),(1,3),(2,3),(3,3)→ 7\times\frac{1}{7}

( 4 , 0 ) , ( 4 , 1 ) , ( 4 , 2 ) , ( 4 , 3 ) , ( 0 , 4 ) , ( 1 , 4 ) , ( 2 , 4 ) , ( 3 , 4 ) , ( 4 , 4 ) → 9 × 1 9 (4,0),(4,1),(4,2),(4,3),(0,4),(1,4),(2,4),(3,4),(4,4)→9\times\frac{1}{9}

→ 1 + 3 3 + 5 5 + 7 7 + 9 9 = 5 \large→ 1 + \frac{3}{3} + \frac{5}{5} + \frac{7}{7} + \frac{9}{9} = 5

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...