An Angle Relationship In This Particular Triangle
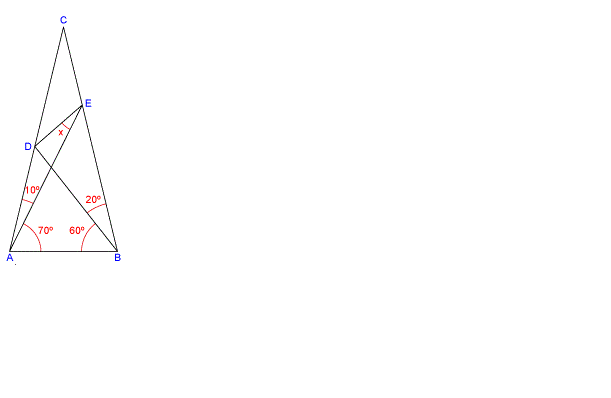 Find
x
(in degrees).
Find
x
(in degrees).
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
dude you just copied your solution from here
Log in to reply
Wow dude, how did you know that?
Log in to reply
because I saw this problem from that source before.
Is this the only way to solve it because I solved it another way.
Log in to reply
If you have another way, Please share.
How is CE=AG?
this problem is too classic.
Why in step 5, FG=FE?
L e t A E i n t e r s e c t B D a t P , a n d X = ∠ P E D . A p p l y s u m o f a n g l e s o f a Δ i s 1 8 0 o . Δ P A B , ∠ B P A = 5 0 . . . . . . . . ( 0 ) Δ D A B , ∠ B D A = 4 0 . Δ E A B , ∠ B E A = 3 0 . ( 0 ) ⟹ ∠ E P B = 1 3 0 . ∴ i n t e r n a l ∠ E D P = 1 3 0 − X . A p p l y S i n e l a w . Δ B D A , A B = A D ∗ S i n 6 0 S i n 4 0 . . . . . . . . . . . . . . . . ( 1 ) Δ B E A , A B = B E ∗ S i n 7 0 S i n 3 0 . . . . . . . . . . . . . . . . ( 2 ) Δ E D A , E D = A D ∗ S i n X S i n 1 0 . . . . . . . . . . . . . . . . ( 3 ) Δ E D B , E D = B E ∗ S i n ( 1 3 0 − X ) S i n 2 0 . . . . . . . . . ( 4 ) F r o m ( 1 ) a n d ( 2 ) B E A D = S i n 6 0 S i n 4 0 S i n 7 0 S i n 3 0 . F r o m ( 3 ) a n d ( 4 ) B E A D = S i n X S i n 1 0 S i n ( 1 3 0 − X ) S i n 2 0 ∴ S i n 6 0 ∗ S i n 3 0 ∗ S i n 1 0 S i n 4 0 ∗ S i n 7 0 ∗ S i n 2 0 = S i n X S i n ( 1 3 0 − X ) = S i n 1 3 0 ∗ C o t X − C o s 1 3 0 . ∴ C o t X = S i n 6 0 ∗ S i n 3 0 ∗ S i n 1 0 ∗ S i n 1 3 0 S i n 4 0 ∗ S i n 7 0 ∗ S i n 2 0 + C o t 1 3 0 X = C o t − 1 ( S i n 6 0 ∗ S i n 3 0 ∗ S i n 1 0 ∗ S i n 1 3 0 S i n 4 0 ∗ S i n 7 0 ∗ S i n 2 0 + C o t 1 3 0 ) = 2 0 o .
From properties of triangle CE/sin10 = CA/sin150 in CAE CD/sin20 = CB/sin 140 in isosceles triangle ABC, CA=CB So CE/CD is available from earlier two relations. So sinCED/sinCDE is available. Also CED+CDE = 160 as DCE = 20 From the above CED comes as 130 So x=150-130 = 20
Draw the circumcircle of △ C D E . Then prove that A E is tangent to the circumcircle and we have x = ∠ C = 4 0 ∘ , by alternate segment theorem.
how to prove AE tangent to circumcircle
Use sine law in triangles: ADE: (sin x)/AD = (sin 10)/DE, ABD: (sin 60)/AD = (sin 40)/AB, and ABE: (sin 30)/AB = (sin 40)/DE. Multipy these equations together to cancel out AD, DE, and AB and derive the equation: sin x = sin 60 sin 10 sin 30 /(sin 20 sin 40), which computes correctly to the answer.
Siine law in ABE should read ABE: (sin 30)/AB = (sin 20)/DE.
CFA with two 20° angles is isosceles, so FC = FA
Draw a line CG, which bisects ACB and conclude: ACG CAE FC-CE = FA-AG = FE = FG FG = FD, so FE = FD