A problem by GH Hardy
1 1 , 1 2 , 2 1 , 1 3 , 2 2 , 3 1 , 1 4 , 2 3 , 3 2 , 4 1 , …
If 1 9 2 0 1 8 8 7 is the m th term and 2 0 1 8 1 7 8 9 is the n th term of the sequence above, find ∣ m − n ∣ .
Note : In this sequence, the fractions do not reduce. For example, 2 2 is distinct from 1 1 .
The answer is 98.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
13 solutions
Thank you to the problem creator. At first I thought we'd have to actually find m and/or n. Sure I could do it, but this is so much easier. I only wonder, why they would want to include the 2 1 ?
Log in to reply
Initially I asked (m-n) but by mistake I posted answer as 49 , so I had to bring the 1/2
Log in to reply
I will update the problem so it is just asking for ∣ m − n ∣ .
Just for fun, m is the term 7242835 and n is the term 7242933.
I have included 1887,1920 intentionally because where there is Hardy, there is Ramanujan
"Incidentally". Upvote from me.
I actually wrote the pattern in a triangle-like sequence. The n th row of the triangle began with (1/n) and as you moved from left to right in the row, the numerator went (1, 2, 3, ..., n) and the denominator (n, n-1, n-2, ..., 1). I did it in about 6 minutes this way. Yours is much nicer.
Okay, I'm quibbling, but I think it should be made clear that this is not a sequence of actual fractional values, since 2 0 1 8 1 8 8 7 reduces to 6 4 0 6 2 9 , and so the difference would be more like 6 4 3 8 7 9 7 , not 9 8 . I went off the rails with that one. Say something to the effect, "don't reduce the fractions".
Log in to reply
Ah, fair point. I will add a note.
Log in to reply
They aren't really fractions at all. They're just ordered pairs - the notation as fractions is a red herring.
I would Like share the same problem quizzes sequences :)
Some of us are not familiar with the notation. It would have been helpful to know what “|m-n|” meant, beyond “the absolute value of m-n” which would have been less than one and obviously not what was expected.
That "incidental" easter egg is indeed a great tribute to Ramanujan.
I was thinking of 1887 as the birth year of a mathematician before I saw your solution.
The sequence consists of infinitely many subsequences in order:
-
1 fraction where the sum of the numbers equals 2,
-
2 fractions where the sum of the numbers equals 3,
-
3 fractions where the sum of the numbers equals 4,
-
...
-
s − 1 fractions where the sum of the numbers equals s ,
-
...
Since 1 8 8 7 + 1 9 2 0 = 1 7 8 9 + 2 0 1 8 , the two given fractions are part of the same subsequence.
Now note that within each subsequence with sum s , the denominators increase 1 , 2 , … , s − 1 while the numerators decrease s − 1 , s − 2 , … , 1 . Since each denominator is one more than the previous one, the distance between two fractions in a subsequence is equal to the difference of their denominators.
In this case, distance = ∣ m − n ∣ = ∣ 2 0 1 8 − 1 9 2 0 ∣ = 9 8 .
The list of numerators and denominators can both be shown in their respective triangular list, like this:
 We want to figure out their position in the sequence:
We want to figure out their position in the sequence:
 (Note that the triangle numbers are on the right-end of each row.)
(Note that the triangle numbers are on the right-end of each row.)
Let N be the numerator, D be the denominator, and R be the row of the n t h term in the sequence.
From the triangle of denominators, we can see that each term is D places after the end of the previous row ( R − 1 ) . Using the triangle number formula 2 n 2 + n , we can find the position from 2 ( R − 1 ) 2 + ( R − 1 ) + D .
Now we need to find the row of the n t h term. To do this, consider the sums of each numerator-denominator pair: they all result in the same distinct numbers for each row. With this, we can find the row for each term using R = N + D − 1 . Substituting this into the formula above gives us:
f ( n ) = 2 ( N + D − 2 ) 2 + ( N + D − 2 ) + D
Plugging 1 9 2 0 1 8 8 7 and 2 0 1 8 1 7 8 9 into this formula, we get 7 2 4 2 8 3 5 and 7 2 4 2 9 3 3 respectively. With these, we can get our final answer: ∣ 7 2 4 2 8 3 5 − 7 2 4 2 9 3 3 ∣ = 9 8
The formule you came up with is correct. However, you divide the end result again by 2. I suppose you ment to calculate the (N+D-2)²+(N+D-2) part, divide it by 2 and then add D and do this 2 times. This gets you: 1887/1920: (1887+1920-2)²+(1887+1920-2)² and this divided by 2 and then + 1920 = 7 242 835 - 7 242 933 = 98 so the last division (which you just added for some reason) by 2 is not correct. An alternative way to quickly verify this is by noticing that the division part in the function is the same since N+D = 3807 for the given divisions. Therefore, the only difference left is just the D's that differ so you get Huge number + 2018 - same huge number - 1920 = 98 and then you could quickly see that the 49 you came up with is just the extra division by 2. All the rest is very well done though!
Log in to reply
When this problem was first put up, it originally asked for |m-n|/2, but it has since been changed. I've updated my answer to match it now, so thanks for pointing it out.
I think you've slipped an extra 2 at the end of the last operation.
This is the longer way to do it, but I did it this way also. Nice puzzle it is.
분모 + 분자 = 3807 나오는데, 시그마 n 공식인 n(n+1)/2에서 m번째와 n번째를 찾으면, {3806(3807)/2 + 1887} - {3806(3807)/2 + 1789} = 1887-1789 = 98
Premise : I'm not English so I'm sorry for any mistake in the text.
First Solution :
1887+1920=1789+2018 => solution: |2018-1920|=98
Second solution :
∣ ( ∑ x = a + b c + d − 1 x ) − ( ( c + d ) − ( a + b ) ) − ( b − 1 ) + ( d − 1 ) ∣ = ∣ ( ∑ x = a + b c + d − 1 x ) + a − c ∣
As b a = 1 9 2 0 1 8 8 7 ; d c = 2 0 1 8 1 7 8 9
Number of jumps performed from the fraction in the serie with denominator equivalent to 1 and sum of numerator and denominator equivalent to (a+b) to the other with same denominator but sum equivalent to (c+d):
( ∑ x = a + b c + d − 1 x )
Number of unnecessary jumps performed in the precedent step:
( ( c + d ) − ( a + b ) )
Offset from the first equation with denominator 1 to the actual fraction b a
( b − 1 )
Offset from the second equation with denominator 1 to the actual fraction d c
( d − 1 )
∣ ( ∑ x = a + b c + d − 1 x ) + a − c ∣ = 9 8
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
|
1 2 |
|
Since denominator+numerator is the same in both terms, the solution simply is 1887-1789=||98||.
The sequence of the numerator can be modeled by a ( x ) = 2 x ( x + 1 ) − x + 1 , where x is the value of the numerator and a ( x ) is equal to the first term at which that value appears in the sequence (where x and a ( x ) are positive integers).
The sequence of the denominator can be modeled by b ( x ) = 2 x ( x + 1 ) , where x is the value of the denominator and b ( x ) is equal to the first term at which that value appears in the sequence (where x and b ( x ) are positive integers).
Now we must account for the fact every positive integer appears multiple times in the sequence. We must write functions to describe the second, third, etc. term that a given value appears in the sequence.
We can account for this in a ( x ) with the function a i ( x ) = a ( x + i ) − x , where i is a positive integer that describes if this is the first ( i = 1 ), second ( i = 2 ), third ( i = 3 ), etc. term at which the value x appears in the sequence.
We account for this in b ( x ) with the function b j ( x ) = b ( x + j − 2 ) + x , where j is a positive integer that describes if this is the first ( j = 1 ), second ( j = 2 ), third ( j = 3 ), etc. term at which the value x appears in the sequence.
To first find m , we plug in our values 1 8 8 7 and 1 9 2 0 into a i ( x ) and b j ( x ) respectively. The term at which a i ( 1 8 8 7 ) = b j ( 1 9 2 0 ) is equal to m .
We find that a i ( 1 8 8 7 ) = b j ( 1 9 2 0 ) at i = 1 9 2 0 , j = 1 8 8 7 .
a 1 9 2 0 ( 1 8 8 7 ) and b 1 8 8 7 ( 1 9 2 0 ) are both equal to 7 2 4 2 8 3 5 , which is the value of m .
Following the same set of steps for 2 0 1 8 1 7 8 9 to find n , we find that a i ( 1 7 8 9 ) = b j ( 2 0 1 8 ) at i = 2 0 1 8 , j = 1 7 8 9 .
a 2 0 1 8 ( 1 7 8 9 ) and b 1 7 8 9 ( 2 0 1 8 ) are both equal to 7 2 4 2 9 3 3 , which is the value of n .
Plugging our values for m and n into ∣ m − n ∣ , we find that ∣ 7 2 4 2 8 3 5 − 7 2 4 2 9 3 3 ∣ = 9 8 .
(m)th no is 1887/1920; (n)th is 1789/2018 here( 2018-1920)=(1887-1789)=98 so started from same number. 1887+1919=3806; If not started from same number
Let as represent them as {A/B} and {C/D},
X)find position of (A/1) as[{(A-1)÷2}×A]+1 【it is the sum of all numbers till (A-1)+1】
●For1887/1920,position of 1887/1 is (1886÷2)×1887+(1)=1779442.from the start ●For 1789/2018,position of 1789/1 is (1788÷2)×1789+(1)=1599367 from the start
Y)find position of A/B from A/1 {A×(B-1)}+[{(B-1)÷2}×B]
●For 1887/1920 it is (1887×1919)+(1919÷2)×1920= 3621153+1842240=5463393 ●For 1789/2018 it is (1789×2017)+(2017÷2)×2018= 3608413+2035153=5643566
So the position of A/B is X+Y from the start,
●For 1887/1920 it is 1779442+5463393=7242835 from start ●For 1789/2018 it is 1599367+5643566=7242933 from start
So the difference is 7242933-7242835=98
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
|
1 2 |
|
Visualising Pascal's triangle makes this much easier. First, calculating the m^th term, 1887/1920. As we know 1/1920 is on the 1920th row, and to get to the row that 1887/1920, you have to add 1887-2 to the denominator, because you dont count the row 1/1920 is on and the row it is actually on. So 1885+1920=3805. Do the same thing for the other number and you also get 3805. Then you the calculate the difference between the two numerators which is -98(m-n), sub into 1/2|(m-n)|, which results in 49
The denominator reset to 1 in every power of 2 going down from the value of that power, so a given number is in a subsequence if their integer value of its log2 is the same. log2(1920) = 10.9068 -> 10 log2(2018) = 10.9787 -> 10 M is bigger than N because is closer to 1
Then their difference would be the same in whichever subsequence they are. In this case, the difference is -98, but being the "lowest" number in a greater position, this number should be taken as positive. Divided by 2 gives us 49 as result.
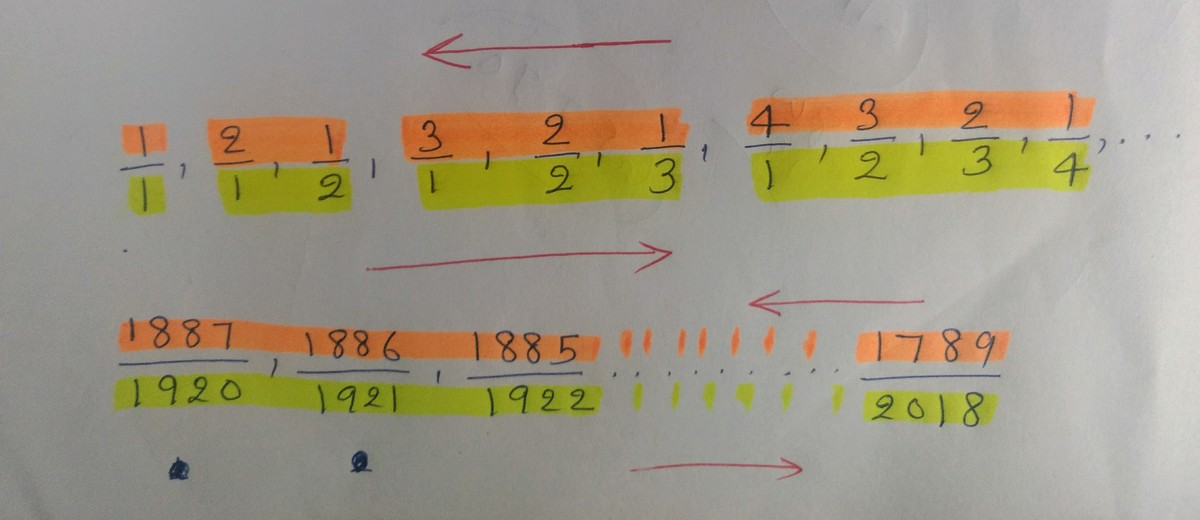
The pattern is that the denominator increases from 1, and the numerator decreases from some integer, n . Then the process repeats with n + 1 .
1 1 , 1 2 , 2 1 , 1 3 , 2 2 , 3 1 , 1 4 , 2 3 , 3 2 , 4 1 , …
Since the denominator increases by 1 while the numerator decreases by 1, the same-colored fractions always have the same sum of numerator and denominator.
Incidentally, the fractions we are given have the same sum of numerator and denominator:
1 9 2 0 1 8 8 7 2 0 1 8 1 7 8 9 : 1 8 8 7 + 1 9 2 0 = 3 8 0 7 : 1 7 8 9 + 2 0 1 8 = 3 8 0 7
Since these sums are the same, they are in the same sub-sequence (as if they were the same color). Then the difference between their indices is 2 0 1 8 − 1 9 2 0 = 9 8 . And so ∣ m − n ∣ = 9 8 .
Incidentally, 1887 and 1920 are the birth-year and death-year of mathematician Srinivasa Ramanujan.