Which box has the gold?
 There are three boxes, but only one of them has gold inside. Additionally, each box has a message printed on it. One of these messages is true and the other two are lies.
There are three boxes, but only one of them has gold inside. Additionally, each box has a message printed on it. One of these messages is true and the other two are lies.
The first box says, "The gold is not here."
The second box says, "The gold is not here."
The third box says, "The gold is in the second box."
Which box contains the gold?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
55 solutions
But in the message said that 1 of them say the true and the other two lies ^_^
Log in to reply
Box 1 was a lie because it said no gold here. Box 2 was true because there was no gold and it said no gold here. The 3rd box was a lie because it said the gold was in box 2 and it was not. The hint was in that two boxes lied and one of them was true. the 2nd box told the truth. So if you pick the 1st box that set the sequence for false truth false.
Yes, so the first box is a lie, the second one is true and the third one is a lie too.
I use guess and check.It is a good solution.
I got this after 2 tries
I am a detective so I am good at things like this so I win
I used guess and check.
good solution
It's the first one (that has the gold).
First, I ran through all of the options. If Box No. 1 was telling the truth, that wouldn't work because if the remaining boxes are lying, then there would be no gold, because No. 3 is lying (The gold is in No. 2) and No. 2. is lying (There is no gold here). That would create a paradoxical statement.
If No. 3 (The gold is in No. 2) is telling the truth, that also wouldn't work because it would mean that No. 1 (There is no gold here) is also telling the truth, which doesn't go together with the True/False/False rule.
So that only leaves No. 2 to be telling the truth, and the gold in Box No. 1.
That's how I figured it out! Again, I may be wrong, because I'm only 12 and not very trained in logic riddles, but this answer seems to make sense to me!
I don't understand. It said that two are lying meaning that since box number 1 and 2 said it isn't here that means box 3 is telling the truth so the gold is in box 2.
I made a truth table as follows:
Box No. 1st 2nd 3rd
If Gold in Box No. 1 0 1 0
If Gold in Box No. 2 1 0 1
If Gold in Box No. 3 1 1 0
In the first row we have two 0's and one 1, which represent two lies and one true statement, thereby fulfilling the conditions prescribed by the problem. Therefore, the gold must be in box 1.
you are right .. it is awesome answer
This is brillant
It is said that one of the boxes has gold and others do not. Also, each box contains a message. In both the first and second box, the message is "The Gold is not here." while the third box has the message "The Gold is in the Second box." . Now, we can have 3 cases : 1) 1st box has true message, 2) 2nd box has true message and 3) 3rd box has true message.
CASE -- 1: If the 1st box has the true message, then there should be no gold in any of the boxes as then the 1st box will not have gold and since 2nd and 3rd box have false message, so the truth for 2nd and 3rd box will be "The Gold is here" and "The Gold is not in the Second box" respectively but the two truths contradict each other. So, CASE -- 1 is not correct.
CASE -- 2: If the 2nd box has the true message, then there should be gold in the 1st box as then the 2nd box will not have gold and since 1st and 3rd box have false message, so the truth for 1st and 3rd box will be "The Gold is here" and "The Gold is not in the Second Box" and then all the truths are not contradictory to each other and are pointing that the gold is in the 1st box. So, CASE -- 2 is correct.
We have got the right case (CASE -- 2), but just for curiosity, lets check out CASE -- 3.
CASE -- 3: If the 3rd box has true message, then there should be no gold in any of the boxes as then the 3rd box will say "The Gold is in the Second box" and since 1st and 2nd box have false message, so the truths of the 1st and 2nd box will be "The Gold is here" and "The Gold is here" respectively. But the 1st and 2nd box both cannot have gold as it is earlier mentioned that only 1 box has gold. So, CASE -- 3 is not correct.
So. we finally have that CASE -- 2 is correct and the gold is in the First Box .
awesome solution..
i did the math in this way. and i found that 2nd case is true and clicked the second box. damn i forgot the other part
Log in to reply
Yes, Case -- 2 is correct, but according to that case, the gold is in the First Box . I can understand how you made the mistake.
you have good future
Log in to reply
I hope so.....thanks for the appreciation.... :)
I clicked the first box it was correct you have to have common sense to answer the question. Clearly the first two boxes said there were not any treasure, but the third box said the second has treasure. The second box said I dont have treasure so clearly the third box is not true. So all you have left is the first box. So i clicked it and it said i was correct. So ur whole explained thing is W.R.O.N.G!
Log in to reply
FFS, read the damn solution first before commenting! I said "Case-2 is correct", not "Gold is in box 2".
"Case-2 is correct" means that the second box has true message and the other boxes have false messages. That directly implies that the gold is in box 1.
There's a easier way to analyze this...so the third box says that there is gold in the second box while the second and first boxes say that they have no gold. So a person may think that the gold is in the 3rd box since it is the only one with a message about where the gold is. However, that's what they want you to think and if you think this far, you are left with choices 1 and 2. but according to the message in the 3rd box, it states that its in the 2nd box which it will most likely not be in. Therefore, you are left with choice 1...at least, that's how I found it :)
Log in to reply
The easiest way to analyze this is by constructing a truth table with the given data. I wrote this solution about 1.5 years ago when I was way more dumber than I am now. I had little but the vaguest idea of truth tables and such stuff back then, hence the lengthy solution.
If I were to write a solution to this problem now, my solution would probably be identical to the one just below my solution (written by Muhammad waseem Anwar).
brilliant prasun biswas
The first box and the second box cannot be both false, since it means the gold is in two boxes. They cannot be both true either, because only one message is true. So one of them is true and the other is false. A false message indicates that the gold is either in the first box or the second box (and hence not the third), and a true message indicates the third box has a false message (because there's only one true message).
The gold is either in the first box or the second box (one of them is false), but not in the second box (third message is false), so it must be in the first box .
EDIT: Shorter solution, inspired from this similar problem:
Box 2 and Box 3 contradict each other. Thus one of them is true and the other is false. Since we have one true statement already, Box 1's statement is false, so the gold is in Box 1.
true
A short yet amazing solution. Why didn't I realize that?
nice
Box 3 and box 2 are contradicting. Thus one of them is false, the other true, leaving one more false message: box 1 . If box 1 is false, thus the gold is there - negating its claim.
( Please keep in mind that there is only one possibility - 1 true and 2 false messages) CASE 1 : Gold in box 1 In this case message in box 1 is false, message in box 2 is true and message in box 3 is false. THIS IS POSSIBLE as we have 1 true and 2 false messages. CASE 2 : Gold in box 2 In this case message in box 1 is true, message in box 2 is false and message in box 3 is true. THIS IS NOT POSSIBLE as we have 2 true and one false messages. CASE 3 : Gold in box 3 In this case message in box 1 is true, message in box 2 is true and message in box 3 is false. THIS IS NOT POSSIBLE as we have 2 true and 1 false message. HENCE ONLY CASE 1 IS POSSIBLE - G O L D I N B O X 1
Yes, this is probably the fastest way to do this. With only three possibilities (gold in the first, second, or third box) it is easy to check which one is correct.
look at the picture. it is in the first box. lol
Haha, that's not the solution to the problem though. Silly of them to provide the answer visually.
The 1st and 2 nd box have the same words so one is true and one is not true ,so the gold must be in either of these 2 boxes. If the 3rd is true then there will be 2 massage true which is wrong so it must be lie so the gold is in the 1 st box
If statement 1 is true, then the gold is not in box one. Assuming that all the others are false, then statement 2 says that the gold is inside, but statement 3 says that it is not, therefore we know that statement 1 is false .
If statement 2 is true, then the gold is not in that box. Statement 1 says that the gold is within box 1 (because it's false, therefore the statement is reversed), and statement 3 tells us that the gold is not in box 2 (again, because it's reversed). So, if statement 2 is true , then it works.
If statement 3 is true, then the gold is in the second box, and statement 2 is reversed so it now says: "The gold is in this box," and statement one says the gold is inside box one. We have two contradicting statements, so we know that statement three is false .
Consider all possibilities:
( 1 , 2 , 3 )
1 ( T , L , L )
2 ( L , L , T )
3 ( L , T , L )
Case 1 is impossible as if Chest 2 lies it would mean that the gold is in Chest 2 , however if Chest 3 also lies it implies that gold is not in Chest 2 . This is a contradiction.
Similarly, case 2 is impossible as since both Chest 1 and 2 have the same statements, it implies that both chests contain gold, which is impossible.
This leaves us with case 3 which we see is the only possible case as the statements on Chests 1 , 2 and 3 . Therefore Chest 1 contains the gold.
- The statements writen on the 2 n d and the 3 r d box contradict each other (one tells 'Box 2 has gold' and the other tells 'Box 2 doesn't have gold'), so one of them must tell the truth, and the other must lie (*).
- On the other hand, the 1 s t and the 2 n d box cannot be both lies (which leads to the gold is in both boxes). Hence, the 3^{rd} box cannot be true.
We can conclude that the 3 r d box lies, and the 2 n d box is true (due to (*) ). Therefore, the 1 s t box lies and it contains the gold.
The message say the gold in second box That is mean second box after third box Which mean the first box
I solved this by reversing the statements to isolate and determine which is the truth. For example if you reverse them, the statements now become:
The first box says, "The gold IS here."
The second box says, "The gold IS here."
The third box says, "The gold is NOT in the second box."
Now, what we've done is created two true statements and one false statement according to the original logic that one is true and the other two are false. Now that we know that two statements are true, we can say that the statements on the second and third boxes cancel each other out because they cannot both be true statements because they directly contradict each other. That leaves us with the statement on the first box which must also be a truth if one false/true statement on the second and third box cancel each other out. Therefore, the gold IS (literally) in the first box.
Not sure if this is the most "textbook" way to solve this, but by reversing the logic of the statements, I was able to solve the "car in the box" problem and "who is the thief" correctly!
So can we just say that we have a set of literals {B1, B2, (NOT)(B2)}(C1, C2, C3). B1 for the first statement and B2 for the second and the last box is a negation of the statement of the second one (NOT)(B2). So we get DNF(disjunctive normal form) as if B1 or B2 or (NOT)(B2) from which we derive empty clause from (C2, C3) and are left with B1. I am just starting to get into this field of study, so please correct me if I am wrong, and this sort of proof can't be applied for this kind of problem
labels: False, True, False.
Golden: full, empty, empty.
All the other combinations do not met the conditions that just one label is correct and only a chest is full of gold.
Make a tree diagram including each of the binary possibilities. Then look for which of them satisfies the requirements of the premise.
Boxes 2 and 3 have contradictory statements, so one must be true, meaning box 1's statement must be false to fulfill the requirement of only one true statement. Therefore the gold must be in box 1.
CASE 1: Box 1 is true. ~If Box 1 is true, ~~ a. Box 1 does not contain the gold. ~~ b. Box 2 is false => It should have the gold. ~~ c. Box 3 is false => It then means Box 2 should NOT have the gold, which contradicts the previous statement (b). ~ergo, Case 1 is INVALID.
CASE 2: Box 2 is true. ~If Box 2 is true ~~ a. Box 2 does not contain the gold. ~~ b. Box 1 is false => It should have the gold. ~~ c. Box 3 is false => It means Box 2 does NOT have the gold, which supports the first statement (a). ~ergo, Case 2 is VALID. (BOX 1 has the gold)
CASE 3: Box 3 is true. ~If Box 3 is true ~~ a. Box 3 does NOT contain the gold but 2 does. ~~ b. Box 1 is false => It should have the gold. ~~ c. Box 2 is false => It should have the gold. ** Only one box should contain the gold, yet there are 2 that exists in this case. ~ergo, Case 3 is INVALID.
Box 1 has the gold. Box 2 statement is true while all others are false.
We can directly eliminate the third option because if gold is in box 2 then statement 1 is correct and same case with gold in box one ....aftr dat we can decide by considering third statement..
Here is the most simple way to approach riddles like that: Rule 1: Whenever one of the actors (in this case the boxes' messages) is stating something about another actor, it's always false, whether the affirmation is positive or negative.
Rule 2: Deduce the rest...
Now in this case since Box 2 is said to be full of gold by box 3 (which is a false statement according to rule 1), box 2 is therefore empty. And so the Gold has to be in box 1, because we now know the box which is telling the truth is box 2. And the two liars are box 1 and 3.
3 cases... case 1 if 1 has the gold then box 1 and 3 lies and box 2 true , case 2 if 2 has the gold then box 1 and 3 true and box 2 lie , case 3 if 3 has the gold then box 1 and 3 true box 2 lie .... so i pick box 1 since it was stated that 2 are lies and 1 is true
Box1 contains gold: then statements 1- wrong, 2- right, 3- wrong. That is two wrong and one right statement. Hence box one contains gold.
if 1st box says true, then 2nd box says lie, and 3rd box says true, so this case is wrong. if 3rd box says true, then 2nd box says lie, and 1st box says lie, so this case is wrong. if 2nd box says true, then 3rd box says lie, and 1st box says lie, so this case is right. so 1st box contains the gold. !!!
- If Gold is in Box 1, 1 & 3 massages are false and 2 is true. Conditions satisfied.
- If Gold is in Box 2, 1 & 3 massages are true and 2 is false. Conditions not satisfied.
- If Gold is in Box 3, 1 & 2 massages are true and 3 is false. Conditions not satisfied. So Gold is in B0x 1
if box 1 has gold then, box 1= FALSE, box 2= TRUE, box 3= FALSE then 1 true and 2 false
IF box 2 has gold then, box 1= TRUE, box 2= FALSE, box 3= TRUE then 2 true and 1 false
if box 3 has gold then, box 1= TRUE, box 2= TRUE, box 3= FALSE then 2 true and 1 false
The box 3 is lie, how did he know in the box 2 has a gold ?? Only box itself who know what is inside exactly. But in the box 3 is empty, why ? If he has gold box 1 and 2 can be true.
The box 2 is true, cuz if he lie and has gold box 1 and 3 can be true.
The box 1 is lie, he has the gold, cuz if he true and the box is empty back to the case box 2 and 3 are impossible to deny. (Absolute)
Note the first and second box cannot both be false as that implies both contain gold which is a contradiction, hence one of the first two boxes must be true.
Next note that the third box must therefore be false, meaning the gold cannot be in the second box and hence, the second box must be true, forcing box one to be false and to be the box containing the gold.
Well, firstly, we notice that both the first and second boxes cannot be true, so the gold must be in one of the first two boxes. So the third box cannot contain the gold. If the third box is correct and the second box contains the gold, then the first box is also telling the truth and we have 2 truths. Thus the second box cannot contain the gold. By process of elimination we see that the first box has the gold, noting also that the first and third boxes are lying, and the second box tells the truth, satisfying the conditions.
We know that 2 messages are lies and 1 message is true.
The first 2 messages are cannot be both lies, since that would mean that the gold is in 2 boxes. If both of the first 2 messages cannot be lies, and both cannot be true, the 3rd message is a lie.
Since the 3rd message is a lie, the gold is not in 2nd box. This makes the 2nd message true.
Therefore the 1st message is also a lie. Therfore the gold is in the 1st box.
the message in the first box say 'the gold is not here' then the second box thought if it say the same message as the first will make us go to the third and say the gold is in it so the message on second box try to play a trick on our mind because it know how our mind use to think on cases like that but message on the third one play a trick too to make us confuse when it say 'the gold in the second' and that make us know that both message of the second is true and the message on the third is a lie and the first box message is a lie too but the message on the third and second make us sur about that the gold in the first one
If the 1st box is true that means there is no gold in the 1st box and 2nd box is lying so it means it has a gold and the 3rd box is saying the lie so it says that there is no gold in 2nd box, so it doesnt make sense, because one says that there is a gold in the 2nd box and another says that there is no gold in the 2nd bix. If the 3rd box is saying the truth, the 1st box is lying so it means 1st box has a gold, and the 2nd box is also lying so it means it has a gold also and the 3rd box is saying the truth so it means that 2nd box as a gold, so it doesnt make any sense, because it mean there us a gold in 1st and 2nd box also. And if the 2nd box is telling the truth the 1st bx is lying so it means that there is a gold in 1st box, and 2nd box is tellling the truth so it means that 2nd box doesnt has a gold, and 3rd is lying so it means that there is no go,d in the 2nd box, so its the only one that has sense and when the 2nd box tells the truth it says that the gold is in the 1st box
This is more of a logic problem than an algebra problem. The way to solve it is to see if the conditions are satisfied.
For three statements, presume the following: Scenario 1: Statement 1 is true and the other two statements are false. But this creates a contradiction, with the gold not in any box if you presume truth in the first statement. Scenario 2: Statement 1 is false, Statement 2 is true and Statement 3 is false. Scenario 3: Statement 1 and 2 are false, and Statement 3 is true. This creates a contradiction again, with the gold not in any box.
By providing true and false values for each statement, only Scenario 2 satisfies the conditions provided. The trick is this though: remember that the first statement is false! i.e. "The Gold is not in this box" is false for Statement 1 actually means that the gold IS in the first box. A little tricky!
SIMPLE see the picture 1st box contains gold and the second box was true that gold is not in there and the 1st and third box were telling lie
First and second both boxes contain the same message,"The Gold is not here". Since only one message is true, one of these two boxes must be true and the other one must be false. Therefore, the third message must be false as already one of the first two messages is true. So the gold is not in the second box. Hence the second box contains true message and the first one contains false. So the gold must be in the first box.
Assume two cases such that in Case 1, the first box's message is true while it is otherwise in case 2.
Case 1 : If first box's message is true, then it follows that Gold is either in the second box or third box and that both of their messages must be false. If Gold is in Box 2, its message is indeed false but Box 3's message will be true. If Gold is in Box 3, its message is indeed false but Box 2's message will be true. Hence, we cannot accept Case 1.
Case 2 : If Box 1 has the Gold, then its message will be false and that either of the message of Box 2 or Box 3 must be true. Box 2 don't have the Gold and so it's message is true; in effect, Box 3's message will be false.
Therefore, Case 2 holds and that Box 1 has the Gold.
There is one message that says that it isn't in the second box, and one that says that it is. If it is there, boxes 1 and 3 are true, so it' not in the second box. So since it's not in the second box, the second box is the truth, and the other 2 are lies. Since the first box says that it's not in the first box, then it is in THE FIRST BOX.
I just solved a problem in 3 lines. Brownie points at least?
A brief solution:
Note that the 2nd and 3rd statements are contradictory. So the true statement must be one of them. This necessarily implies that the 1st statement is false. But if the 1st statement is false, then the 1st box must contain the gold.
Second box - "gold is not here" or "gold is not in second"
Third box - "gold is in second"
One is lie, other is truth.
So, first has to be lie. (as there are two lies) Thus gold is in first box.
Easiest way - See the picture.
CASE 1: gold in box 2 ..... message 1:true, message 2: false, message 3 : true ...... 2 true 1 false..... case invalid CASE 2: gold in box 3 ..... message 1:true, message 2: true, message 3 : true ...... 2 true 1 false..... case invalid
If the gold is not in box 2 and 3, it must be in 1
One said the truth and other two lied so.Take the last statement which says "the gold is in the second box" either he is telling the truth or lying .case1 if he is telling the truth than 2nd box must be lying as only one box tells the truth..but the second box also say the other version of 3rd's statement "gold is not here" therefore 3rd is false ..so gold is not in the second box it's in the first and second is telling the truth as 1st is also lying about gold
Assume that the message in the third box is true. This implies that the message in the first box is true. Similarly, we can rule out the second and third boxes. Hence, the gold is in the first box.
its simple 2nd and 3rd arguments are contradictory to each other, hence it can be concluded that one of them is telling the truth while other one lies. since we have already got one truth teller who is among either 2 or 3, it means 1 is definitely a liar since there are two liars. since 1 is lying that it is not having gold the truth is that it has gold.
case 1- true, lie, lie------------------> here as the first msg is true, we can assume that the gold is in 2nd and 3rd box. As 2nd msg is a lie, we can say that the gold is in 2nd box. But unfortunately 3rd msg is also a lie, and it says the gold is in 2nd box which turns out to be true. So this case is wrong.
case 2- lie, true, lie--------------------> here the 1st msg is a lie, so we know that the gold is in the first box. the second msg is true, and it is correct in saying that the gold is not here. 3rd msg is also a lie and as 2nd box doesn't contain gold this is correct.
So case 2 is correct and our solution is box 1. I didn't bother to check case 3 :p
If the first case is to be believed, then gold is not in the first box, thus gold has to be in the second box (since it says gold is not here) and it does not have to be in the second box (since the third box says that the gold is in the second box), which is not possible.
If the second box is to believed, then the gold is not in the second box, this is validified by the statement of the the third box (since it is a lie), and the first box says that the gold is not there which is a lie, so the gold is in the first box.
And finally, is the third box is to be believed, then, according to the statements of box 1 and 2, gold has to be there in both the boxes which is not possible since gold is there in only one box.
Hence, answer is the the first box and the second statement is true.
Just make binary table , taking three variables box1, box2, box3. and then select the combination of two false and one true.. you will get three cases (True,False,False) (False,True,False) AND (False,False,True), then notice that first case cannot exist because this combination goes against rule. notice that in the last two rules first box always is FALSE, that is it speaks lie, that means when he says that he doesnot have the gold, he certainly HAS THE GOLD!!! arrest him ..heheh
Just do trial and error considering one statement true and the other 2 false each time. If you consider the second statement true then, the gold is not in the 2nd box. Then the 1st statement that 'gold is not here' is false. Therefore the gold IS there. The 3rd statement that ' the gold is in the second box ' is also a lie. Therefore , the gold is in 1st box. If you consider any of the other two statements as true it will lead to a paradox. try it and see. pretty simple
There are three conditions
1. True False False
2. False True False
3. False False True
check all the 3 conditions
The second one holds correct
If the first box says it doesn't have the gold then its saying false and it contains the gold
Second box says it doesn't have gold , he is telling true
Third box says it doesn't have a gold and he says False
Correct situation is second one and the Answer is Box 1
1st clue- We know that any one of the boxes contain the gold
2nd clue- We know that only one of the messages is true.
1st box- I don't contain gold
2nd box-I don't contain gold
3rd box-The gold is in second box.
1st step- Now the message of the 3rd box has to be false because if the message is true then the message of 1st box has to be true and we know that only one message can be true.
2nd step-Now let's consider the 1st message to be true then the message on the second and third box has to be false but if the message on 2nd box is false then it says-'I have gold' and the message on 3rd box is false too so it says -'the 2nd box doesn't have gold' now this creates a confusion if 2nd message is true then 3rd has to be false or vice-versa.
3rd step-Now let's consider the message on the 2nd box to be true then the 1st box message and 3rd box message is false now 1st box says-'I have gold' but this not the end to the problem it might again create the same confusion like in step 2 but this confusion won't happen in the 3rd step because 3rd box says - 'the gold is not in second box' that means the gold could be in the 3rd box too but then the message of 1st box will be true and again we cant have more than 1 true message so the 1st box will have the gold.
Suppose, the message of 2nd and 3rd box are lies.
So , the true statement for 2nd box is * "The gold is here (in the second box)" *(minus multiplied by minus is plus).
Now, the correct statement for 3rd box is "The gold is not in the second box" .(plus multiplied by minus is minus).
But it cannot be at the same time.
So, two of this messages must be true. Total number of lies is 2.One is the 2nd or 3rd box message.
There is 1 lie left. So it must be the 1st box message. So, 1st box message is false.
The first box says, "The gold is not here".
If this is false then obviously the gold is in the 1st box.
We can consider Three cases:
CASE (I):
Let us assume that the message on the third box is true .
Therefore, the gold is in the second box. Hence, the message on second box is false. As the gold is in 2nd box, the 1st and 3rd box are empty. Hence the message on 1st box is also is true. So, messages on two boxes, 1st and 3rd are true, but it contradicts the fact that only 1 message is true.
So our assumption is wrong.
CASE (II):
Let us assume that the message on the 1st box is true .
Hence, the gold can be in 2nd or 3rd box.
(i) If gold is in 2nd box, then message on box 3 is also true.
(ii) If gold is in 3rd box, then message on box 2 is also true.
So our assumption is wrong.
CASE III:
Let us assume that the message on the 2nd box is true .
Hence, the gold can be in 1st or 3rd box.
(i) If the gold is in 1st box, then messages on 1st and 3rd box are false.
(ii) If the gold is in 3rd box, then message on box 1 is true.
HENCE IN THE ABOVE THREE CASES, (i) OF CASE (III) SATISFIES THE GIVEN CONDITIONS OF THE QUESTION.
*HENCE THE GOLD IS IN THE * F I R S T B O X **
The messages on the second and third box contradict each other, so one of them has to be true. Thus the message on the first box is definitely false and the gold is in the first box.
if it was the first one, it would contradict itself but for the second, it shows that it is first 3 also contradicts itself
If both 1 & 2 were lies, that would be impossible because then both would have treasure, and as we already know the treasure is only inside one of them . This means that the untruthful chests are either 1 & 3 or 2 &3. But if 2 & 3 *were false, that would mean the 3rd chest is actually saying there is no treasure in 2, while 2 would have the treasure, causing contradiction. But if 1 & 3 were false , 1 would have the treasure and 3 was lying, while 2 is telling the truth that there is no gold inside it. Therefore, the treasure is inside Chest 1.
1 and 2 cannot both be true as we are then left with too many true statements, and they can't both be false since it will mean that there are gold in both which is not allowed either. So either 1 or 2 is telling the truth, and the gold is the one that lies. In any case we already have a true statement so therefore 3 is lying, so the gold is not in 2, and must therefore be in 1.
wll i guess
The First and second box can't both lie otherwish it would mean that they both contain the gold ,So we can conclude one of them tell the true and then we can tell The third box must lie . If The third box lie then the Second box tell the true. We conclude that the First box lie and must contain the gold.
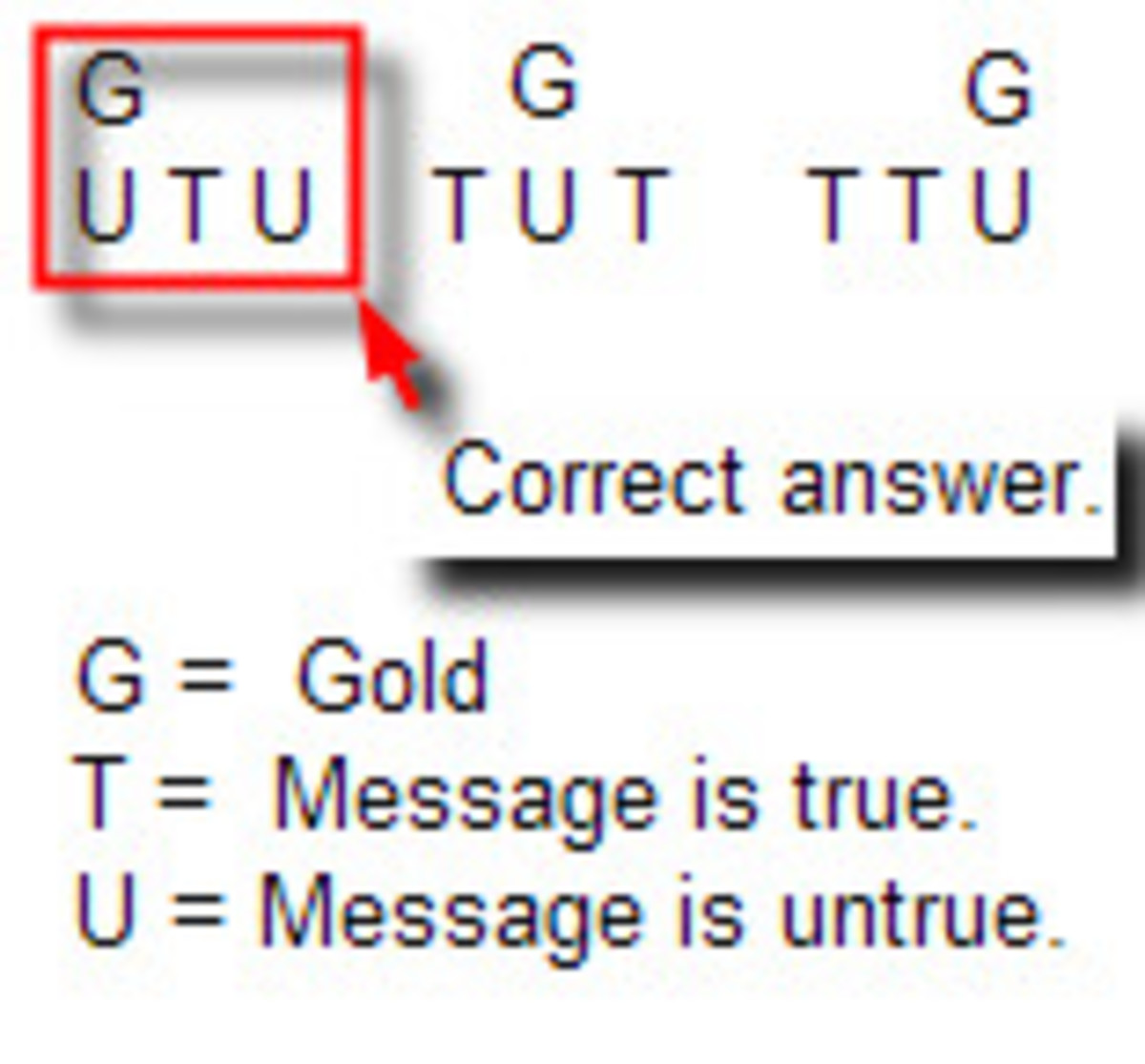
If we assume that the gold is in the first box, then we see the following sequence for the dialogues:
False, True, False. This sequence agrees with the condition of one truth and two lies, but we'll look at the other possibilities for completeness.
If we assume that the gold is in the second box the sequence will be,
True, False, True. But this is not possible given that we were told two statements are false.
If we assume that the gold is in the third box the sequence will be,
True, True, False. Again, this set of answers is not possible because two answers are true.
The conditions are met only for the first scenario, which implies that the first box has the gold in it.