Raising the flag
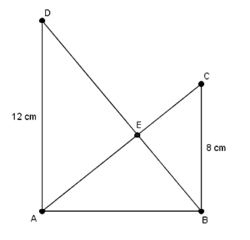 Figure above shows two right triangles
and
with right angles at
and
respectively. With
is the point of intersection between the straight lines
and
. If we drop a straight line from
that is perpendicular to the base
and intersect at
at point
, find the distance
in
.
Figure above shows two right triangles
and
with right angles at
and
respectively. With
is the point of intersection between the straight lines
and
. If we drop a straight line from
that is perpendicular to the base
and intersect at
at point
, find the distance
in
.
The answer is 4.8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
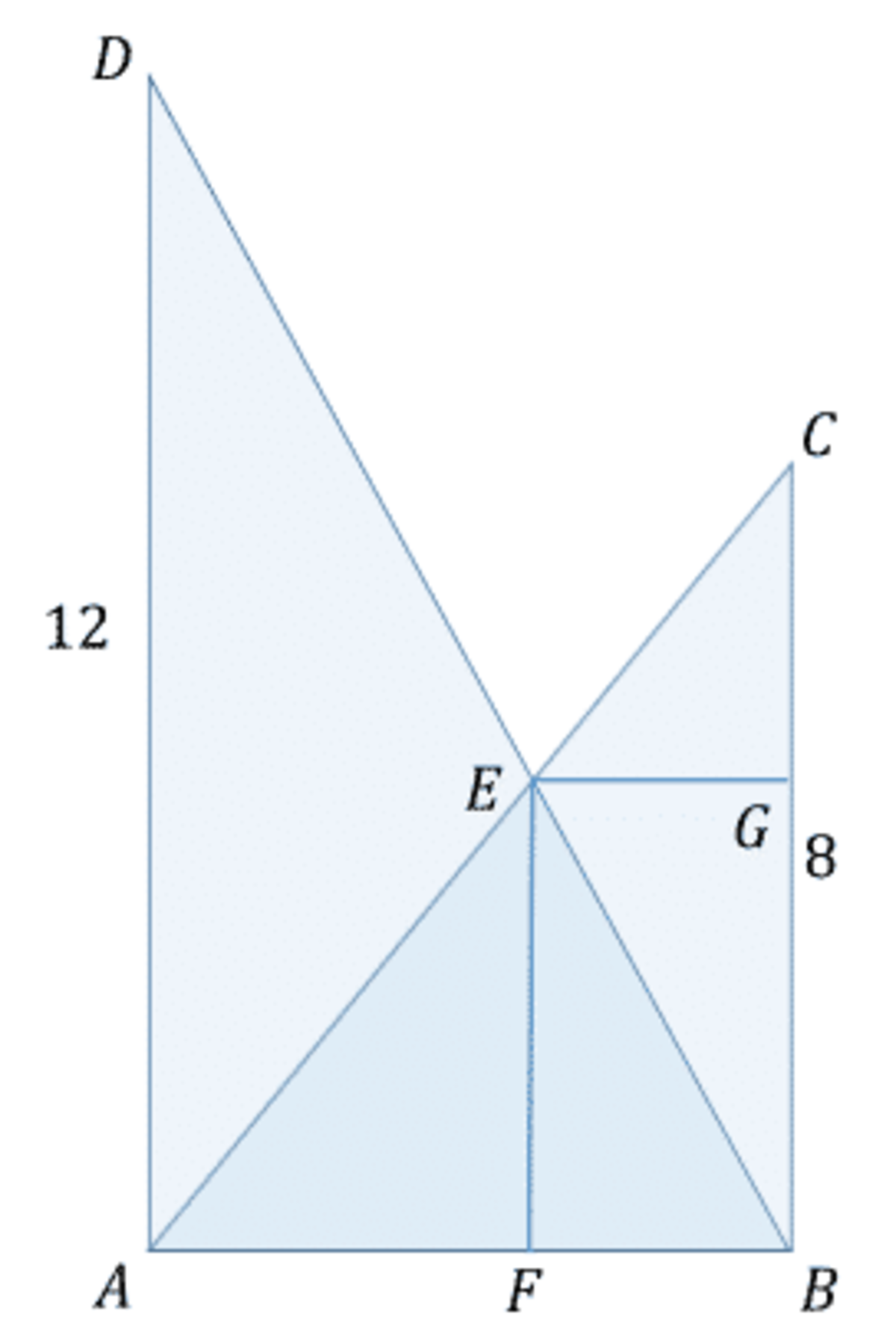
FB/EF=(AF+FB)/12 and AF/EF=(AF+FB)/8 by similar triangles solve both for AF+FB then set them equal 12FB/EF=8AF/EF therefore AF=3FB/2 eliminate AF using the above relation so, (3FB/2)/EF=(5FB/2)/8 eliminate FB's and get EF=24/5 It is interesting to note that as the poles are moved farther and farther apart EF does not change height.