Professor's stone

Classical Mechanics Level 3

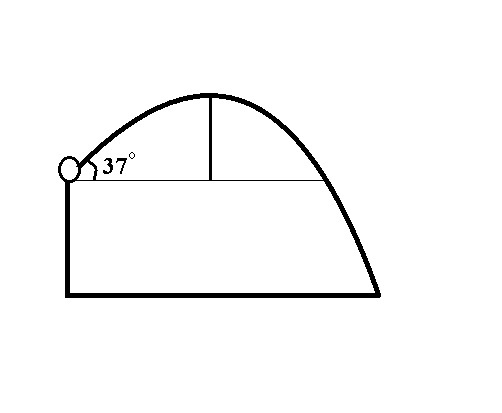
A 6-ft physics professor, standing on the edge of the a 40-ft high building, throws a stone with a velocity of 50 ft/s at an angle of 37 degrees above the horizontal.

Neglecting air resistance what is the speed of the stone just before it hits the ground?

80.56 73.78 66.35 90.81

View wiki
James Guevara by James Guevara , 22, Philippines

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

James Guevara
Nov 20, 2016

V x = V o c o s θ = 50 c o s 37 Vx = Vocosθ = 50cos37

V y 2 = ( V o s i n θ ) 2 − 2 g y Vy^2=(Vosinθ)^2 - 2gy

V y 2 = ( 50 s i n 37 ) 2 − 2 ( 32 ) ( − 46 ) Vy^2 = (50sin37)^2 -2(32)(-46)

V = √ ( V x ) 2 + ( V y ) 2 V=√(Vx)^2+(Vy)^2

= 73.78 f t / s = 73.78 ft/s

2 Helpful 0 Interesting 0 Brilliant 0 Confused

The angle is actually completely irrelevant to this problem if you just solve it using energy concepts.

Steven Chase - 4 years, 6 months ago

Log in to reply

Without an angle we can solve for the velocity before it hits the ground by using the formula (1/2)(mva^2)+mgh=(1/2)mvd^2 where va is 50 ft/s and vd is the unknown. we can cancel the m and put the values. (1/2)(50^2)+(32)(46)=(1/2)vd^2;vd= √2(1250+1472) ;vd=73.78 ft/s

James Guevara - 4 years, 6 months ago

I also did the same thing. I mistakened with value of g

Md Zuhair - 3 years, 11 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...