A calculus problem by Jose Sacramento
n → ∞ lim n k = 1 ∑ n k + 1 k = ?
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Great.. Thanks Chew-Seong Cheong. Cheers
Generalisation of this problem:
Proposition.- If the sequence ( a n ) n = 1 ∞ fulfills n → ∞ lim a n = a where a is a finite number, then n → ∞ lim n ∑ k = 1 n a k = a Sketch of Proof.- Applying Stolz-Cesaro Theorem if a = 0 . If a = 0 it is "trivial" q.e.d □
In this case, lim k → ∞ k + 1 k = 1 ⇒ n → ∞ lim n ∑ k = 1 n k + 1 k = 1
Other example.- n → ∞ lim n ∑ k = 1 n ( k + 1 ) 2 2 k 2 = 2
The sum will become a large number added by infinity The n will be infinity Those two devided by one other Gives 1
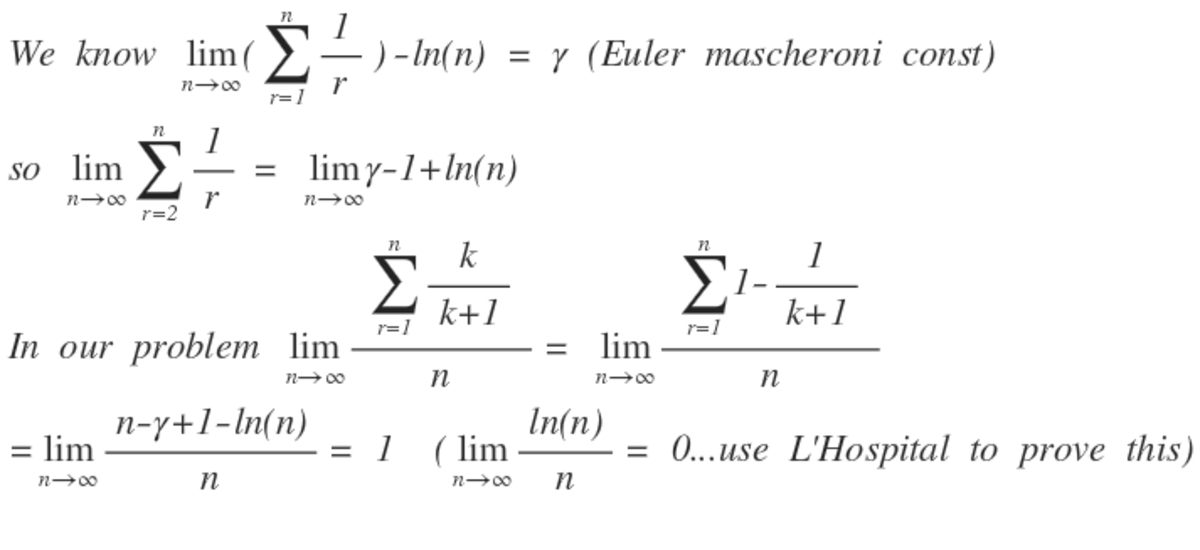
The limit can be found using Stolz–Cesàro theorem as follows.
Theorem 1 (the ∞ / ∞ case) :
Let ( a n ) n ∈ N and ( b n ) n ∈ N be two sequences of real numbers such that
(a) 0 < b 1 < b 2 < ⋯ < b n < ⋯ and n → ∞ lim b n = ∞ .
(b) n → ∞ lim b n + 1 − b n a n + 1 − a n = l ∈ R .
Then, n → ∞ lim b n a n exists and is equal to l .
In this case, a n = k = 1 ∑ n k + 1 k and b n = n . Therefore,
n → ∞ lim b n + 1 − b n a n + 1 − a n = n → ∞ lim ( n + 1 ) − n ∑ k = 1 n + 1 k + 1 k − ∑ k = 1 n k + 1 k = n → ∞ lim 1 n + 2 n + 1 = n → ∞ lim n + 2 n + 1 = n → ∞ lim 1 + n 2 1 + n 1 = 1