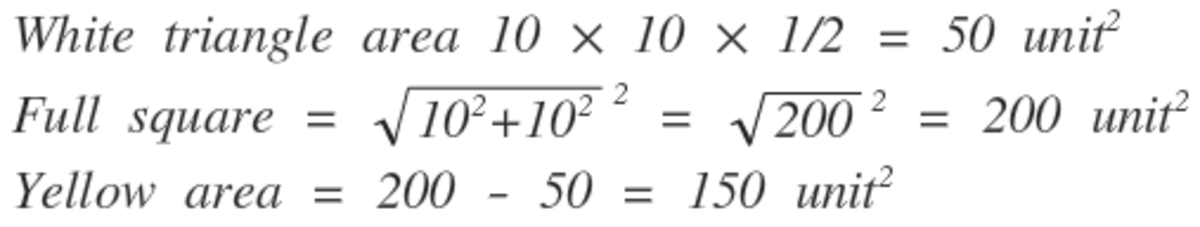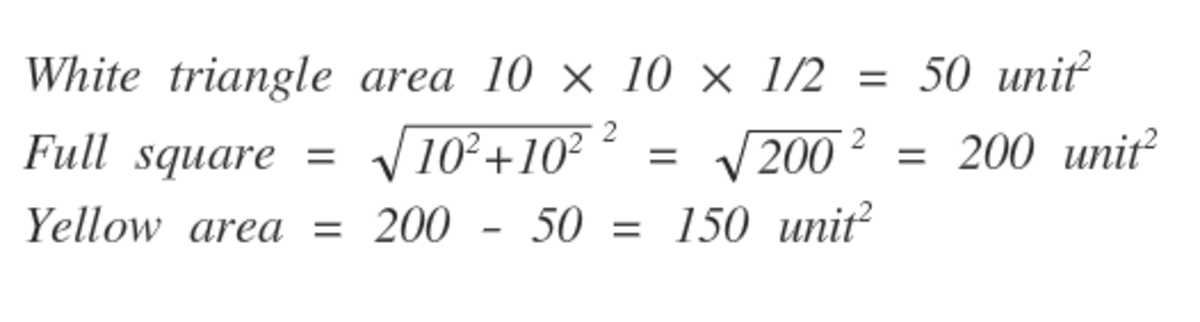Can You Find The Yellow Area?

Let A be the hypotenuse of the white triangle.

Then $A = \sqrt{10^2 + 10^2} ≅ 14.14$ .

But A = B , which is the side of the square, so the area of the square is $14.14^2 ≅ 200$ .

The area of the triangle is simply $\frac{10 \times 10}{2}$ .

So finally, the yellow area is $200 - 50= \boxed{150}$ .

Edited for formatting purposes

Using Pythagoras $X= \sqrt{10^{2}+10^{2}}= \sqrt{200}=10 \sqrt{2}$

The area of the square is $X^{2}= 200$

The area of the triangle is $\frac{1}{2} \times b \times h = \frac{1}{2} \times 10 \times 10$

Hence the yellow area is $200 -50 = 150$

Relevant wiki: Pythagorean Theorem

Area of triangle=(1/2)bh=(1/2) * 10 * 10=50 square units

x=sqrt(10^2+10^2) using Pythagoras theorem

x=sqrt(200)

Area of square=x*x =sqrt(200) * sqrt(200) =200 square units

Therefore the area of yellow region =Area of square - Area of triangle = 200-50=150 square units

Area of squar = X^2 = 200 ------------------(1) Area of trangle = 1/2 × 10 ×10 = 50 -------(2) Area of yellow region = 200 - 50 = 150