A problem by Kalpit Jain
Level
pending
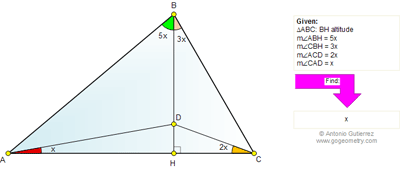Given a triangle ABC. BH is an altitude drawn on opposite side AC at H. (see the figure). <ABH=5x, <CBH=3x, <DAH=x and <DCH=2x. Find x(in degrees).
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
AH:CH = tan 5x : tan 3x and also AH:CH = tan 2x : tan x
tan 5x tan x = tan 3x tan 2x
sin 5x cos 3x cos 2x sin x = cos 5x sin 3x sin 2x cos x
(sin 8x + sin 2x)(sin 3x – sin x) = (sin 8x - sin 2x)(sin 3x + sin x)
sin 8x : sin 2x = sin 3x : sin x (by componendo & dividendo)
sin 8x sin x = sin 3x sin 2x
sin 8x = 2 sin 3x cos x = sin 4x + sin 2x
sin 8x – sin 4x = sin 2x
2 cos 6x sin 2x = sin 2x
cos 6x = 1/2
6x = 60 deg
x = 10 deg