A probability problem by Krishneel Donz
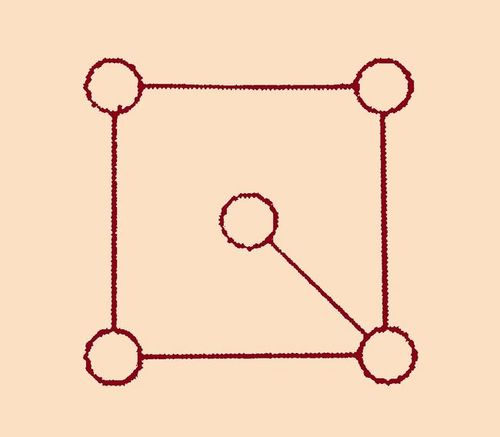 The diagram shows five discs connected by five line segments. Three colours are available to colour these discs. In how many different ways is it possible to colour all five discs if discs which are connected by line segment are to have different colours?
The diagram shows five discs connected by five line segments. Three colours are available to colour these discs. In how many different ways is it possible to colour all five discs if discs which are connected by line segment are to have different colours?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
No matter which one you take to start, it's the same. So it figures you're right.
Just note that any permutation of the valid coloring is also a valid coloring. Hence number of valid coloring should be divisible by 3 ! = 6 . This leaves only one choice.
But lets say the choices weren't given. Then how would you go about solving it?
Log in to reply
but that wasn't the case, was it? the 1st priority is to reach the accurate solution, the 2nd priority is to reach it in the minimum number of steps. also when you learn something you learn the basic theory first then the special cases, while solving is the opposite, you 1st search for special case if applicable then try the basic theory
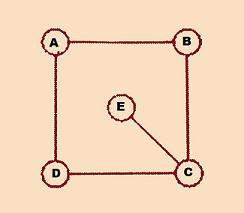
Circle E can be paint of 3 colors, C , B and D of 2 colors, in total 2 4 ways then for select which will be the color of A are to cases:
1 ) B and D are the same color ⇒ there are 2 ways.
2 ) B and D are different colors ⇒ there is 1 way.
For first case are 1 2 × 2 = 2 4 ways and for the second are 1 2 × 1 = 1 2
∴ are 3 6 different ways
3*2=6........what` divisible by 6 and just less than 40-->36
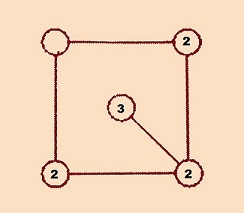
It all starts with the middle disc. For the middle disc there are 3 ways of coloring it. And corresponding to the middle disc only one out of the 3 discs that are not joined with the middle one should have the same color as that of the middle one. hence it follows like this ; Middle disc; 3 Disc connected to middle one; 2 Disc connected to above one in either direction {up or left}; 3 The last disc remaining ; 2 Hence the answer is 36
in the simplest possible format, probability is done by multiplication - the middle one has 3 options - the one attached to it has 2 options - (that's 6 so far) - the next two have 4 options, assuming the middle is A and the next is B, then they can be AA, CC, AC, CA - the last one's probability depends on the preceeding, it has 2 options if AA or CC, and 1 option if AC or CA - the propability can be then calculated by splitting those 4 options in the folowing form:
probability=(3x2x2x1)+(3x2x2x2)=36