A geometry problem by Leonardo Joau
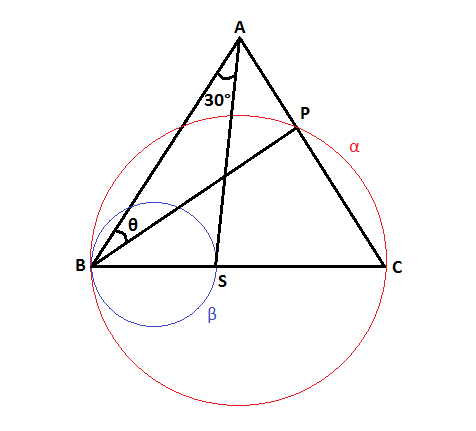
A B C is an isosceles triangle with A B = A C .
α and β are two circumferences that have centres in B C and intersects this straight line in points B , S and C .
The diameters of α and β are 2 + 1 and 1 , respectively.
If ∡ B A S = 3 0 ∘ find ∠ A B P .
Enter your answer in degrees.
Note: Image drawn not up to scale.
The answer is 15.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Let angle B A C = θ . Let O be the center of α . Draw radius P O of circle α . Since P O C is isosceles and with vertex at O , and A B C and P O C share angle A C B , we can conclude that A B C ≅ P O C , therefore P O C = θ . Since angle P B C is the inscribed angle of P O C , then we can conclude that P B C = 2 P O C = 2 θ . But, since angle A B C = 9 0 − 2 θ and A B P + P B C = A B C , then we can equate the two to get 9 0 − 2 θ = A B P + 2 θ , giving us A B P = 9 0 − θ .
Let angle S A C = γ . We get that 3 0 + γ = θ . By sin law on triangle A B S , sin 3 0 S B = sin A S B A B . Also, by sin law on triangle A S C , sin γ S C = sin A S C A C . But, since S B = 1 , S C = 2 , sin A S B = sin A S C (sines of supplementary angles are congruent), A B = A C , we can combine the two equations above to give us sin 3 0 S B = sin γ S C , which simplifies to sin γ = 2 1 , or γ = 4 5 .
Since γ = 4 5 , t h e t a = 3 0 + γ = 3 0 + 4 5 = 7 5 . Also, since A B P = 9 0 − θ , A B P = 9 0 − 7 5 = 1 5 .
Therefore, our answer is 1 5 ..
We have B S = 1 and S C = 2 and sin ∠ A B C = sin ∠ A C B .
By Applying Sine Law on Triangles A B S and A C S ,
1 sin 3 0 ∘ = A S sin ∠ A B S = A S sin ∠ A C S = 2 sin ∠ S A C
Therefore ∠ S A C = 4 5 ∘ . Let M be the point of intersection of A S and B C . We see that ∠ A M P and ∠ A M B are supplementary. Since P is a point on α , ∠ A P B = ∠ B P C = 9 0 ∘ . This gives us ∠ A M P = 4 5 ∘ , ∠ A M B = 1 3 5 ∘ and ∠ A B P = 1 5 ∘
Here, B S = 1 ; S C = 2 . Now, applying sine rule in triangles ABS and ACS yields s i n 3 0 ∘ B S = s i n ∠ C A S S C So, ∠ C A S = 4 5 ∘ . Triangle CPB is inscribed in a semicircle. Hence, ∠ C P B = ∠ A P B = 9 0 ∘ . Finally, from triangle APB, we have ∠ A B P = 1 5 ∘ .