Limiting Angle
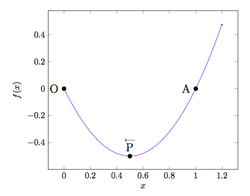 A
(
1
,
0
)
is a point on the parabola
y
=
2
x
(
x
−
1
)
. From point
A
, point
P
is moving along the curve towards the origin
O
(
0
,
0
)
. What is the limit
P
→
O
lim
sec
∠
A
P
O
?
A
(
1
,
0
)
is a point on the parabola
y
=
2
x
(
x
−
1
)
. From point
A
, point
P
is moving along the curve towards the origin
O
(
0
,
0
)
. What is the limit
P
→
O
lim
sec
∠
A
P
O
?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
We can also use vectors to find the angle between vectors PA and PO.
The slope at the origin is − 2 (I used calculus to get that so I guess I sorta cheated). Let angle A O P = θ . Then
tan θ = − 2 . In this case θ is negative but we will take the positive value of theta for our purposes.
Note that as point P approaches point O ∠ P A O approaches 0 . This means that the limiting value of ∠ A P O = 1 8 0 − θ , call it α . We may realize that
tan α = 2 − 1 .
Now we may construct a right triangle with sides 2 and 1 and hypotenuse equal to 5 (by the Pythagorean Theorem ), and from here it is simple to deduce that sec α = 5 − 1 .
Recall: The slope m ( P O ) of the secant line P O is the average rate of change between P and O lim P → O m ( P O ) = Slope of the tangent line at point O
What the problem is essentially asking is the secant of the angle between the tangent line at point O and the line O A .

To solve the problem we need to find the angle θ using the dot product of T and O A . To do this we must first find vector T .
m ( x ) = d x d ( 2 x ( x − 1 ) ) = 4 x − 2 and m ( 0 ) = − 2 T = ⟨ − 1 , 2 ⟩ and O A = ⟨ 1 , 0 ⟩ Note: To find vector T just choose two points on the line y = -2x, e.g (-1,2) and (0,0), and subtract their components.
Now that we have the two vectors we can solve the problem.
T ∙ O A = − 1 ∣ T ∣ = 5 ∣ O A ∣ = 1 T ∙ O A = ∣ T ∣ ∣ O A ∣ c o s ( θ ) → c o s ( θ ) = ∣ T ∣ ∣ O A ∣ T ∙ O A = 5 − 1
Finally: s e c ( θ ) = c o s ( θ ) 1 = − 5
My solution involves finding ∠ A P O in terms of the co-ordinates of point P and then taking the limit as P → O .
Let P ≡ ( t , 2 t ( t − 1 ) ) , as it lies on the parabola y = 2 x ( x − 1 ) .
Slope of O P , m 1 = t − 0 2 t ( t − 1 ) − 0 = 2 ( t − 1 ) .
Slope of P A , m 2 = t − 1 2 t ( t − 1 ) − 0 = 2 t .
Let ∠ A P O = θ , then ∣ tan θ ∣ = ∣ ∣ ∣ 1 + m 1 m 2 m 2 − m 1 ∣ ∣ ∣ .
Since sec 2 θ = 1 + tan 2 θ , we have sec θ = ± 1 + ( 1 + 4 t ( t − 1 ) 2 ) 2 .
Observe that as P → O , t → 0 ; and also ∠ A P O > 9 0 ∘ , so sec ∠ A P O < 0 .
P → O lim sec ∠ A P O = − t → 0 lim 1 + ( 1 + 4 t ( t − 1 ) 2 ) 2 = − 5 .
There must be other ways to solve this, but I found this method quite traditional.
First of all,
Letting ∠ A P O = α ,
If sec α has a limit, then sin α also has a limit. Thus, we shall first find \displaystyle\sin\alpha).
Consider a general point P ( x , y ) , which lies on the given parabola.
It is clear that,
y = 2 x ( x − 1 )
Using Sine Rule,
O A sin α = A P sin ∠ A O P
Thus,
1 sin α = A P x 2 + y 2 y = ( x − 1 ) 2 + y 2 x 2 + y 2 y
Substituting y = 2 x ( x − 1 ) , we get,
sin α = ( 4 x 4 − 8 x 3 + 5 x 2 ) ( 4 x 4 − 8 x 3 + 5 x 2 − 2 x + 1 ) 2 x ( x − 1 ) = ( 4 x 2 − 8 x + 5 ) ( 4 x 4 − 8 x 3 + 5 x 2 − 2 x + 1 ) 2 ( x − 1 )
Note that we cancelled out the x 's, which is why we could not just substitute the final x-coordinates i.e x = 0
Now, substituting x = 0 , because, as the problem suggests, finally, x → 0
sin α = 5 − 2
⇒ cos α = ± 5 1
We reject the positive value, because, when P approaches O , clearly, ∠ A P O > 9 0 o
⇒ sec ( A P O ) < 0
Thus,
sec α = − 5