A geometry problem by Matteo Ruth
In △ A B C is ∣ A B ∣ = 1 0 , ∣ B C ∣ = 1 8 and ∣ C A ∣ = 1 3 . Choose A ′ on [ B C ] , B ′ on [ A C ] and C ′ on [ A B ] that the bisectors of △ A B C perpendicular are on the sides of △ A ′ B ′ C ′ like on the picture.
How long is [ A ′ B ] ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
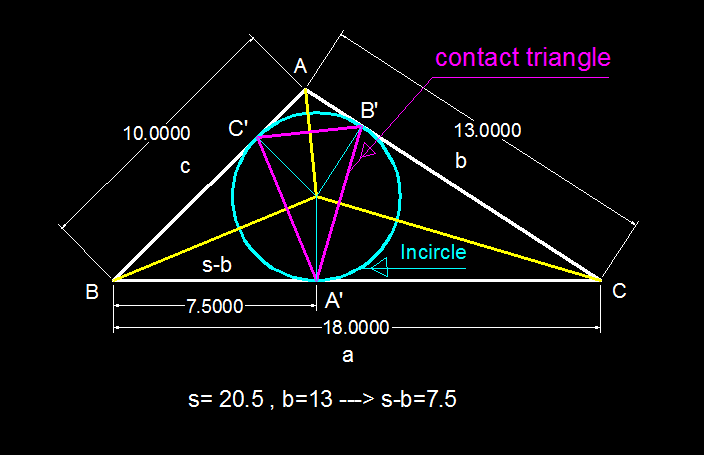
Again a beautiful solution. +1)
Let B A ′ = x , C B ′ = y and A C ′ = z . This implies that, C A ′ = 1 8 − x , A B ′ = 1 3 − y and B C ′ = 1 0 − z . Now we find in the figure above that each pair of the right triangles that share a common side are congruent ( ASA ). This leads us to a system of a three variable linear equations:
1 0 − z = x . . . ( 1 ) 1 8 − x = y . . . ( 2 ) 1 3 − y = z . . . ( 3 )
Solving for x yields that x = 7 . 5
Nice alternate short and simple approach.
No question that Ahmad Saad 's solution is far better that the below solution. But different {long !) approach.
I
n
Δ
A
B
C
,
∠
B
=
C
o
s
−
1
2
∗
1
0
∗
1
8
1
0
2
+
1
8
∗
2
−
1
3
2
=
C
o
s
−
1
2
4
1
7
.
.
.
C
o
s
L
a
w
.
r
=
s
e
m
i
p
e
r
i
m
e
t
e
r
A
B
C
a
r
e
a
A
B
C
=
2
4
1
4
1
∗
4
1
∗
1
5
∗
5
∗
2
1
=
4
1
5
∗
4
1
7
.
∴
B
A
′
=
C
o
t
(
2
1
∗
C
o
s
−
1
2
4
1
7
)
∗
4
1
5
∗
4
1
7
=
7
.
5
.
This is how I first tried to resolve it. But I was sure that there was a other solution. But great tho! Nice job!
We can see that A B ′ = A C ′ , B ′ C = A ′ C , B C ′ = A ′ B
A B = A C ′ + B C ′ = 1 0 . . . ( 1 ) B C = A ′ B + A ′ C = 1 8 . . . ( 2 ) A C = A B ′ + B ′ C = 1 3 . . . ( 3 )
- ( 1 ) + ( 2 ) − ( 3 ) :
( A C ′ + B C ′ ) + ( A ′ B + A ′ C ) − ( A B ′ + B ′ C ) ( A C ′ + A ′ B ) + ( A ′ B + A ′ C ) − ( A C ′ + A ′ C ) A C ′ + A ′ B + A ′ B + A ′ C − A C ′ − A ′ C 2 ∗ A ′ B A ′ B A ′ B = 1 0 + 1 8 − 1 3 = 1 5 = 1 5 = 1 5 = 1 5 / 2 = 7 . 5