A classical mechanics problem by Md. Nure Alam
Four persons K, L, M, and N are initially at the four corners of a square of side 'd'. Each person now moves with a uniform speed of 'v' in such a way that K always moves directly towards L, L directly towards M, M directly towards N and N directly towards K. At what time will the four persons meet?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
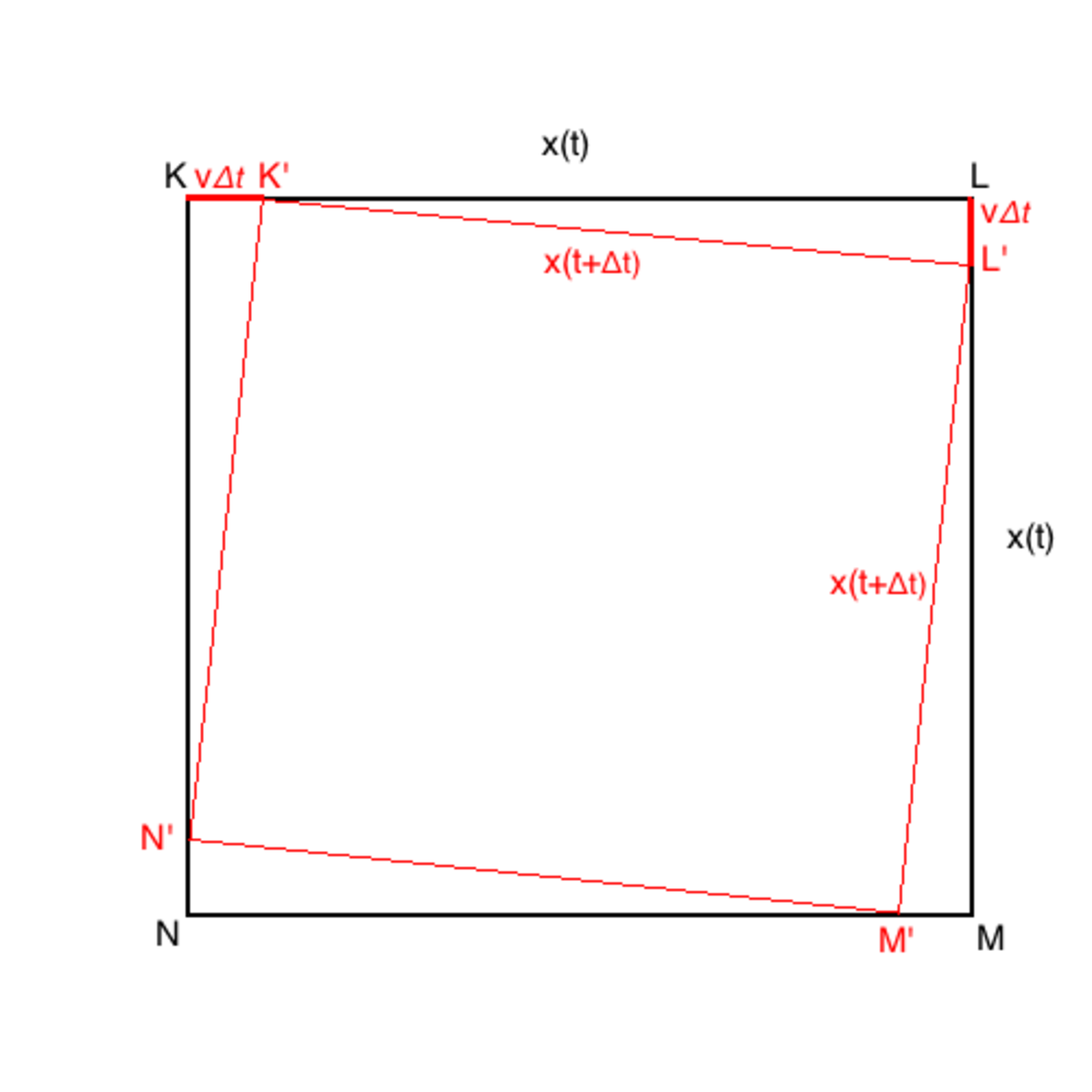It is not hard to show that the red shape must also be a square. This is not surprising but important for our calculation. Let's take the square at an arbitrary time t, with side lengths x(t). Notice that we have a right triangle with side lengths x(t)−vΔt, vΔt, and x(t+Δt). Using the pythagorean theorem, we obtain the equation:
x(t+Δt)2=(x(t)−vΔt)2+(vΔt)2
Expanding the squared equations we get:
x(t+Δt)2=x(t)2−2x(t)vΔt+2(vΔt)2
Now, let α(t)=x(t)2:
α(t+Δt)=α(t)−2α(t)−−−−√vΔt+2(vΔt)2
More algebra, move α(t) over, divide by Δt
α(t+Δt)−α(t)Δt=−2α(t)−−−−√vΔt+2(vΔt)2
Now notice if we let Δt go to 0 (which represents continuous motion), the left side is just a derivative:
dα(t)dt=−2α√vΔt
Now this is just a differential equation that is easy to solve with separation of variables:
dαα(t)√=−2vΔtdt
Note, our integral over α(t) will go from d2 to x(t)2.
∫x(t)2d2dα(t)α(t)√=∫t0−2vΔtdt
(2α(t)−−−−√)x(t)2d2=−2vt
|x|−|d|=−vt
Now we can solve for t when x=0 (d is assumed to be positive, so we drop the absolute value):
t=d/v
