An algebra problem by Naman Choudhary
3 9 + 4 5 + 3 9 − 4 5 = ?
Give your answer to 3 decimal places.
The answer is 3.000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Moderator note:
Thanks for the edit. Wonderful and neat as always. Keep up the good work!
By the way, a better to explain it by showing that S is a real number so its discriminant is non-negative.
Nice solution sir!
set it equal to z, cube the whole thing Some Fundemental polynomials that we need to know 1. (a+b)^3 = a^3 +3a^2 b + 3a b^2 + 3b^3 2. (a+b)(a-b) = a^2 -b^2 If we substitute a for cuberoot(9+4sqrt(5)) and b for cuberoot(9-4 sqrt(5)), z^3 expanded, we get (9+4sqrt(5)) + 3 cuberoot(9+4sqrt(5))^2 * cuberoot(9-4sqrt(5)) + 3*cuberoot(9-4sqrt(5))^2 * cuberoot(9+4sqrt(5)) + (9-4sqrt(5)
now we use the second expansion formula (9+4sqrt(5)) (9-4sqrt(5)) = 81-81 =1 so z^3 = (9+4sqrt(5)) + 3 1 cuberoot(9+4sqrt(5)) + 3 1*cuberoot(9-4sqrt(5)) + 9-4sqrt(5) if we simplify, we get z^3 = 18 + 3cuberoot(9+4sqrt(5)) + 3(9-4sqrt(5))
now we divide everything by 3,
z^3 / 3 = 6+cuberoot(9+4sqrt(5)) + (9-4sqrt(5))
that second part, cuberoot(9+4sqrt(5)) + (9-4sqrt(5)), is what we set to z
so the difference between z^3 / 3 and z = 6
z^3 /3 - z = 6
(z^3 - 3z)/3 = 6
z^3 -3z-18 = 0
Now we use the rational root theorem, the possible roots are plus minus 1, 3, 9, 18
we plug in and we get positive 3 as the answer...
P.S. Sorry, I don't know latex yet, so I put my solution in a picture
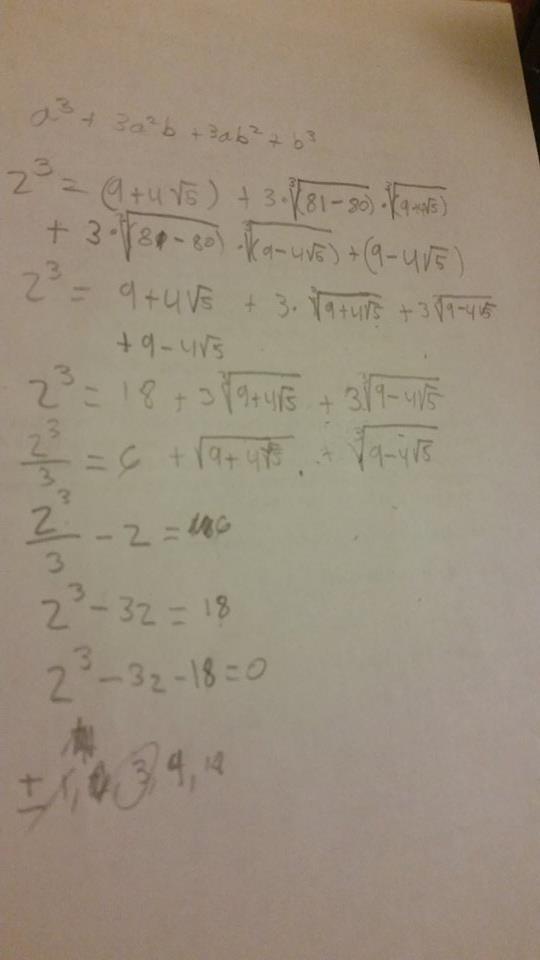
Let 3 9 + 4 5 + 3 9 − 4 2 5 − x = 0 c o n s i d e r a = 3 9 + 4 5 , b = 3 9 − 4 5 , c = ( − x ) I f a + b + c = 0 t h e n a 3 + b 3 + c 3 = 3 a b c 3 9 + 4 5 3 + 3 9 − 4 5 3 + ( − x ) 3 = 3 ( 3 9 + 4 5 . 9 − 4 5 ) . ( − x ) 9 + 4 5 + 9 − 4 5 − x 3 = 3 3 8 1 − 8 0 ( − x ) 1 8 − x 3 = 3 . 1 . ( − x ) 1 8 − x 3 = − 3 x x 3 − 3 x − 1 8 = 0 B y f a c t o r i z i n g w e g e t , ( x − 3 ) ( x 2 + 3 x + 6 ) = 0 x − 3 = 0 x 2 + 3 x + 6 = 0 , Δ < 0 x = 3 T h e r o o t s a r e c o m p l e x . B u t t h e s u m o f t w o i r r a t i o n a l s c a n n o t b e c o m p l e x ∴ 3 9 + 4 5 + 3 9 − 4 5 = x = 3
Let A = 3 9 + 4 5 , B = 3 9 − 4 5 and S = A + B = 3 9 + 4 5 + 3 9 − 4 5
Now,
S 3 = = = = ( A + B ) 3 A 3 + 3 A 2 B + 3 A B 2 + B 3 A 3 + B 3 + 3 A B ( A + B ) A 3 + B 3 + 3 A B S ⇒ ( ∗ )
Thus,
A 3 + B 3 = = = ( 3 9 + 4 5 ) 3 + ( 3 9 − 4 5 ) 3 9 + 4 5 + 9 − 4 5 1 8
3 A B = = = = = 3 ( 3 9 + 4 5 ) ( 3 9 − 4 5 ) 3 3 ( 9 + 4 5 ) ( 9 − 4 5 ) 3 3 8 1 − 8 0 3 3 1 3
Instead A 3 + B 3 with 1 8 and 3 A B with 3 in equation ( ∗ )
S 3 = S 3 − 3 S − 1 8 = ( S − 3 ) ( S 2 + 3 S + 6 ) = S = 1 8 + 3 S 0 0 3
From equation
S 2 + 3 S + 6 = Δ = 0 3 2 − 4 ( 1 ) ( 6 ) = − 1 5
Δ < 0 . Thus, this equation has no real solution.
Hence, 3 9 + 4 5 + 3 9 − 4 5 = 3